Introduction
不存在完美的analysis
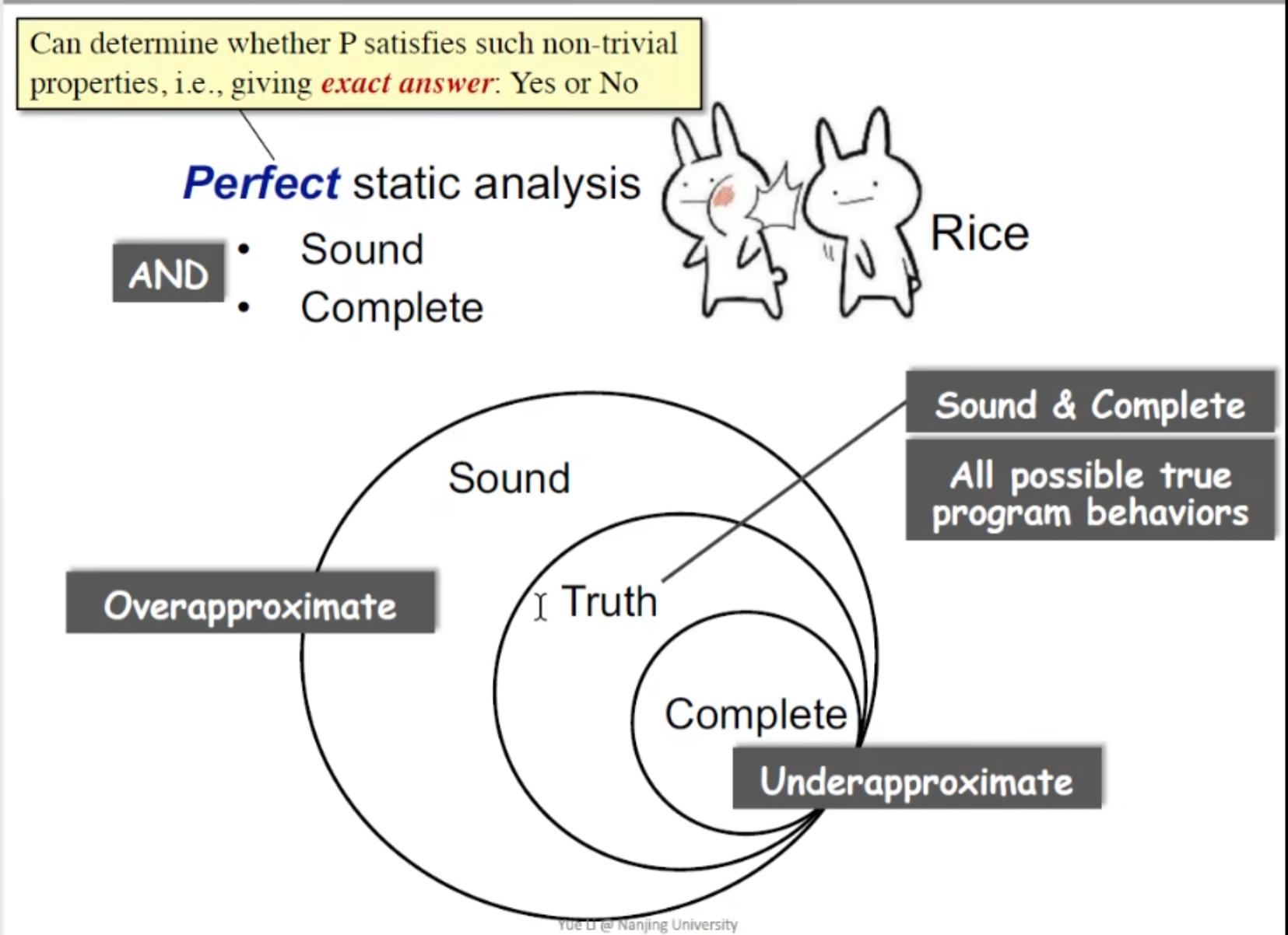
定义有用的静态分析:

sound / complete ,与漏报/ 误报有关,也会和后面讲到的 may /must analysis 相关,大部分静态分析都是妥协sound的,也就是存在误报
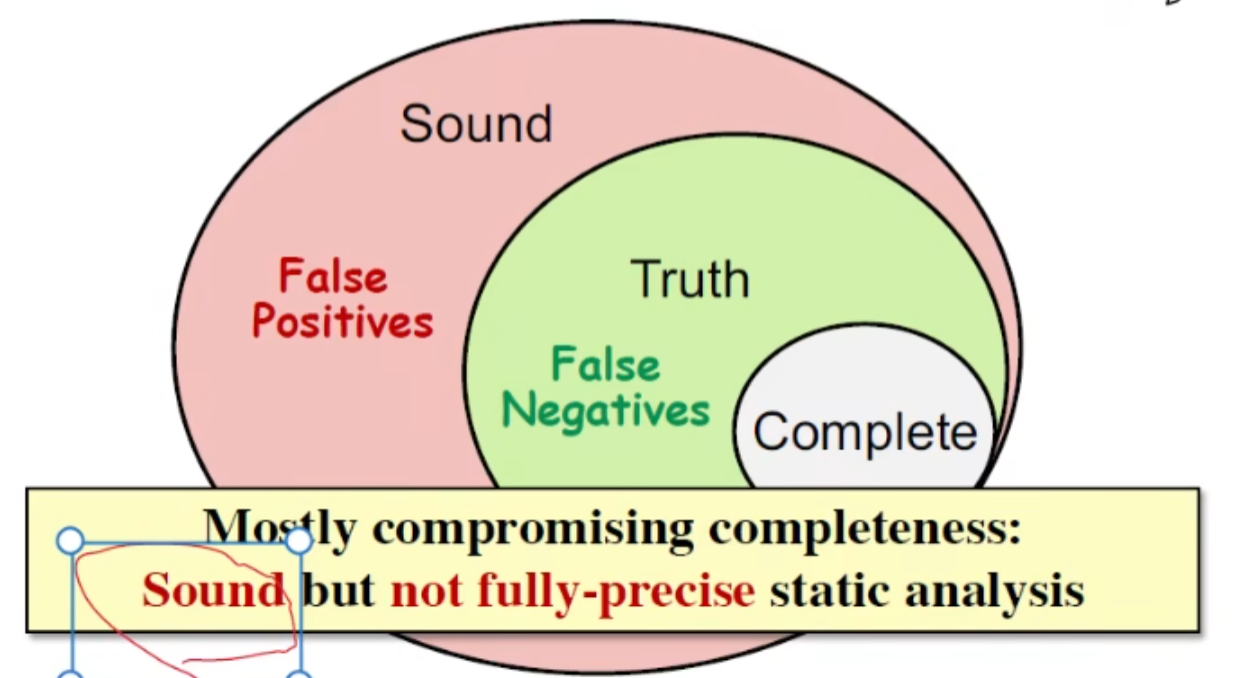
原因:
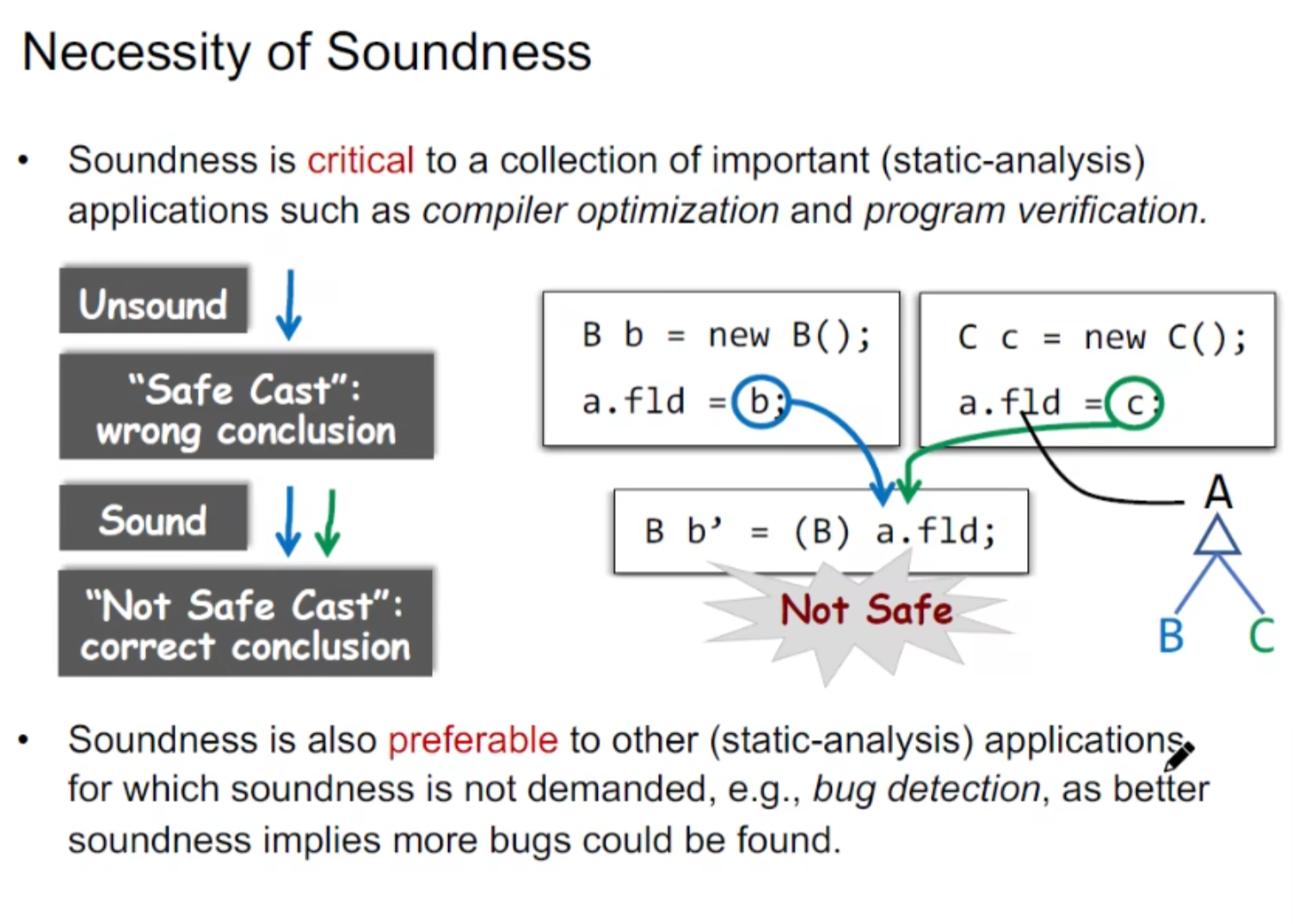
IR
编译器与静态分析:
静态分析是在IR层面上分析的(3AC / SSA 等)
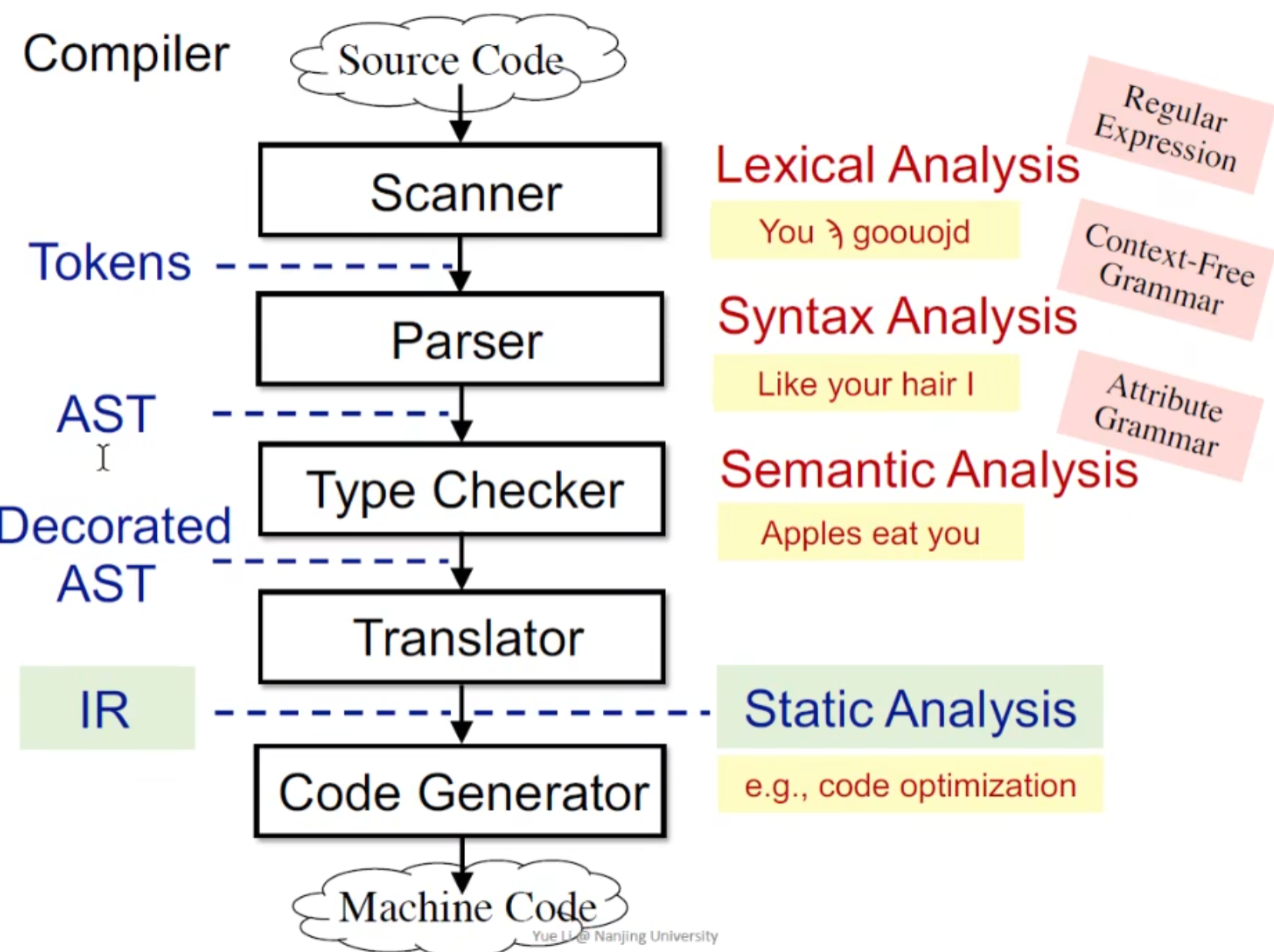
为什么不在AST 语法树层面分析
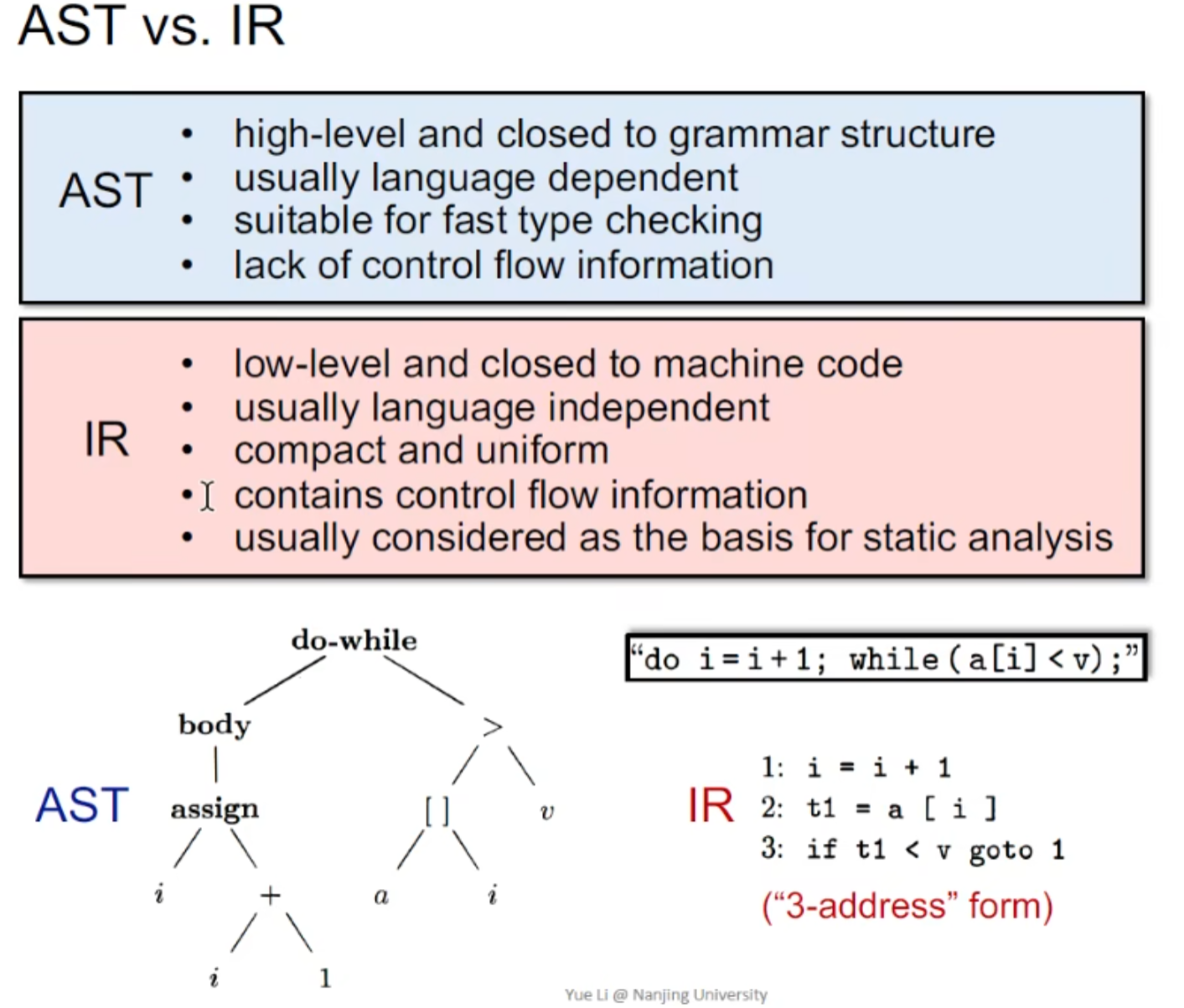
- 语言无关更好,不同语言的AST可能完全不同
- 更接近底层机器码,适合优化
- 更直观 ,可以看出CFG
- IR通常作为静态分析的基础
然后有一大段关于java的一点点入门分析 主要是Soot相关,看视频了解一下即可 ,略过。
3AC与SSA

SSA不是我们关注的重点

如何构建BB
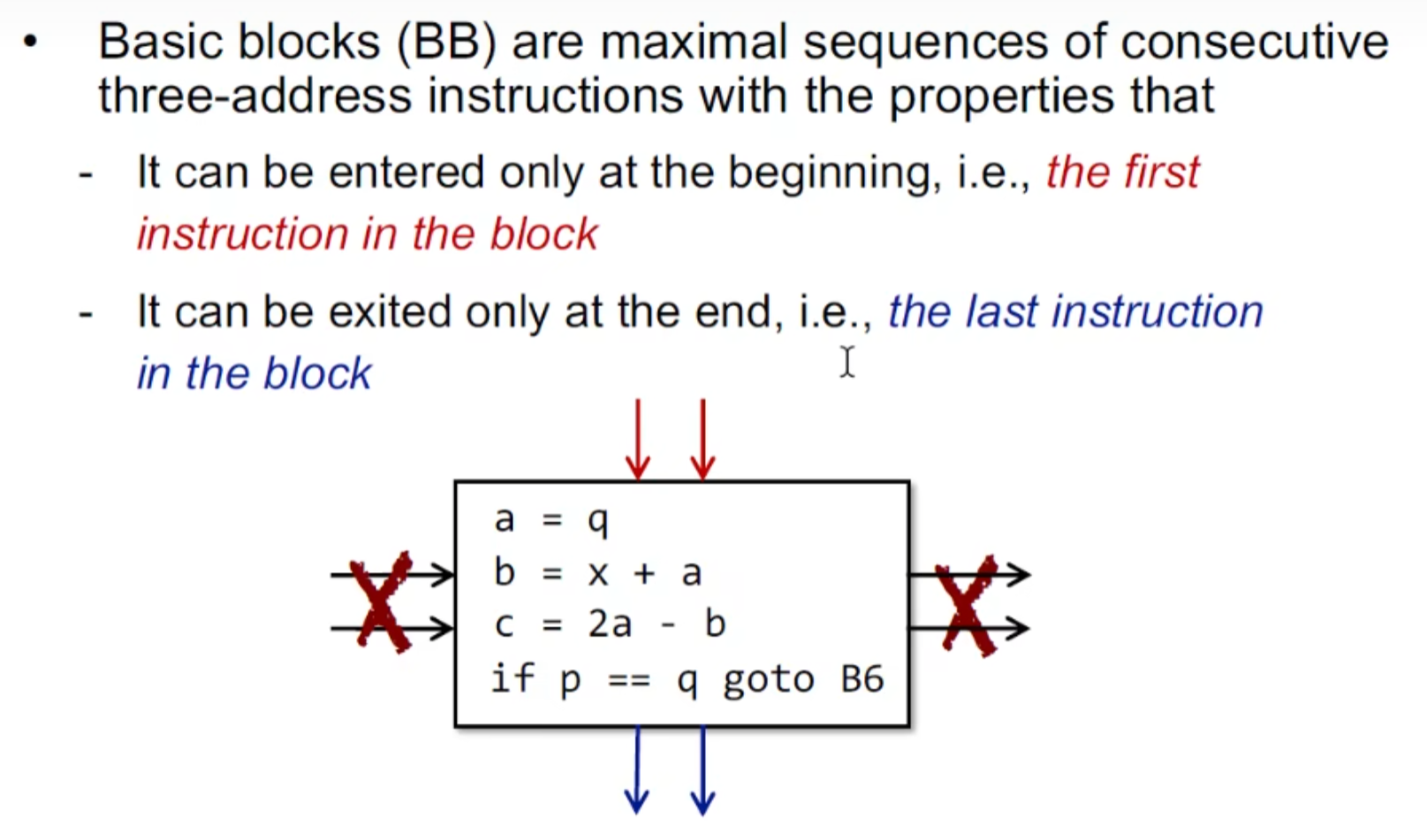
主要就是确定入口

- 第一条指令是入口;
- 任何跳转指令的目标地址是入口;
- 任何跟在跳转指令之后的指令是入口。
非常好理解

如何构建CFG

主要就是三种:
- goto 直接跳转
- 条件跳转有两个出口
- A,B相邻,且A结尾不是无条件跳转 (这时候B可能是别的语句的跳转目标啥的 , A -> B 直接连就行)
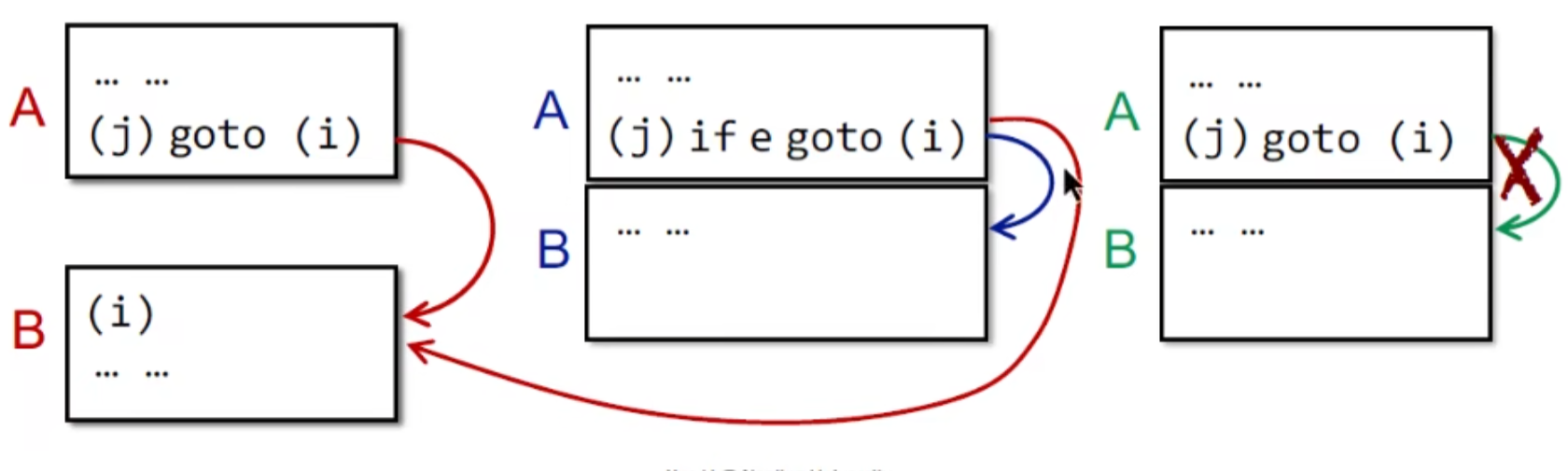
这里的一些概念: 边 Edges, 前驱 predecessor , 后继successor
还要给程序加上出入口,静态分析才能运行(类似状态机有个初始状态?)
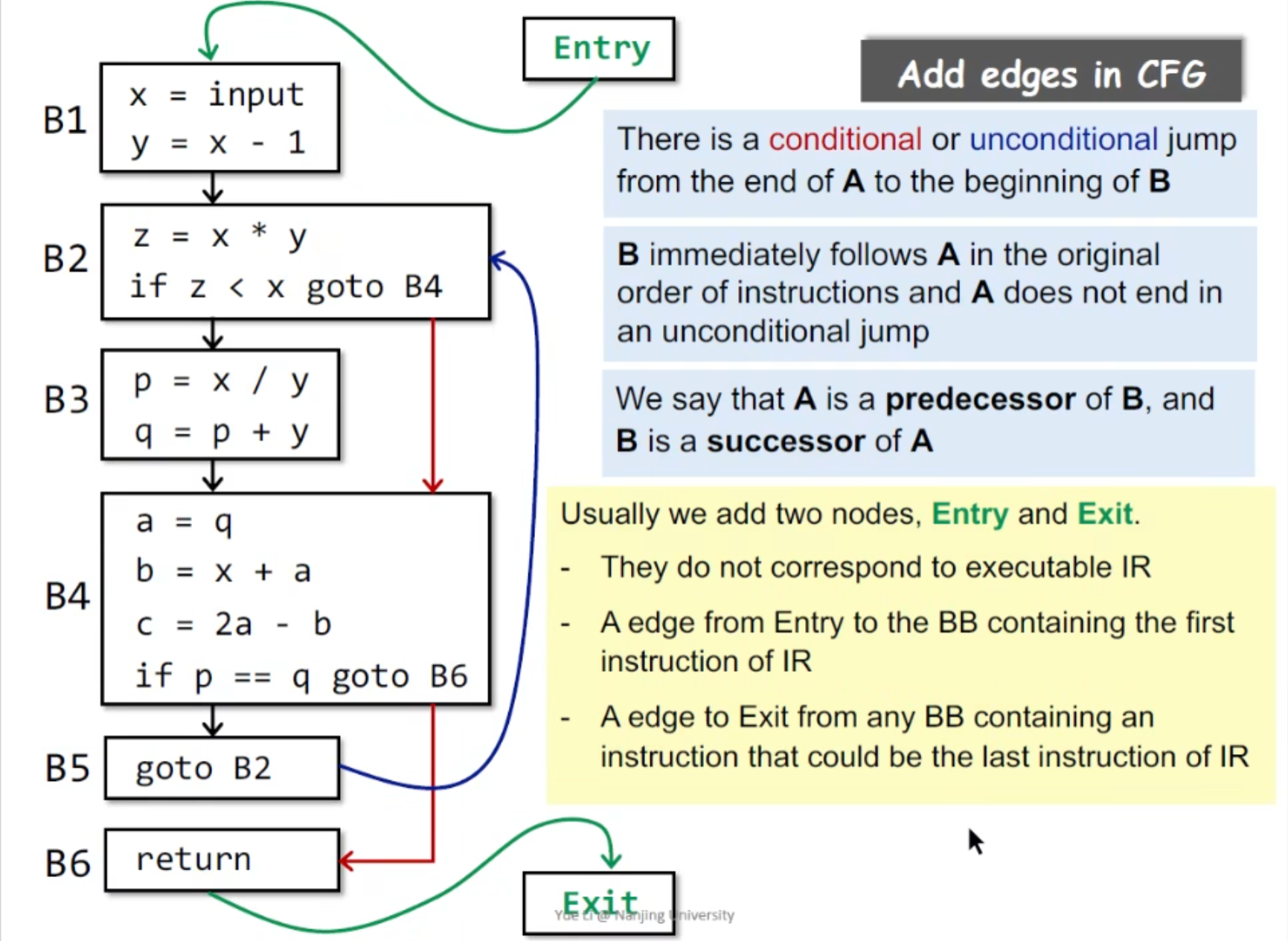
Dataflow Analysis
数据流分析
定义:


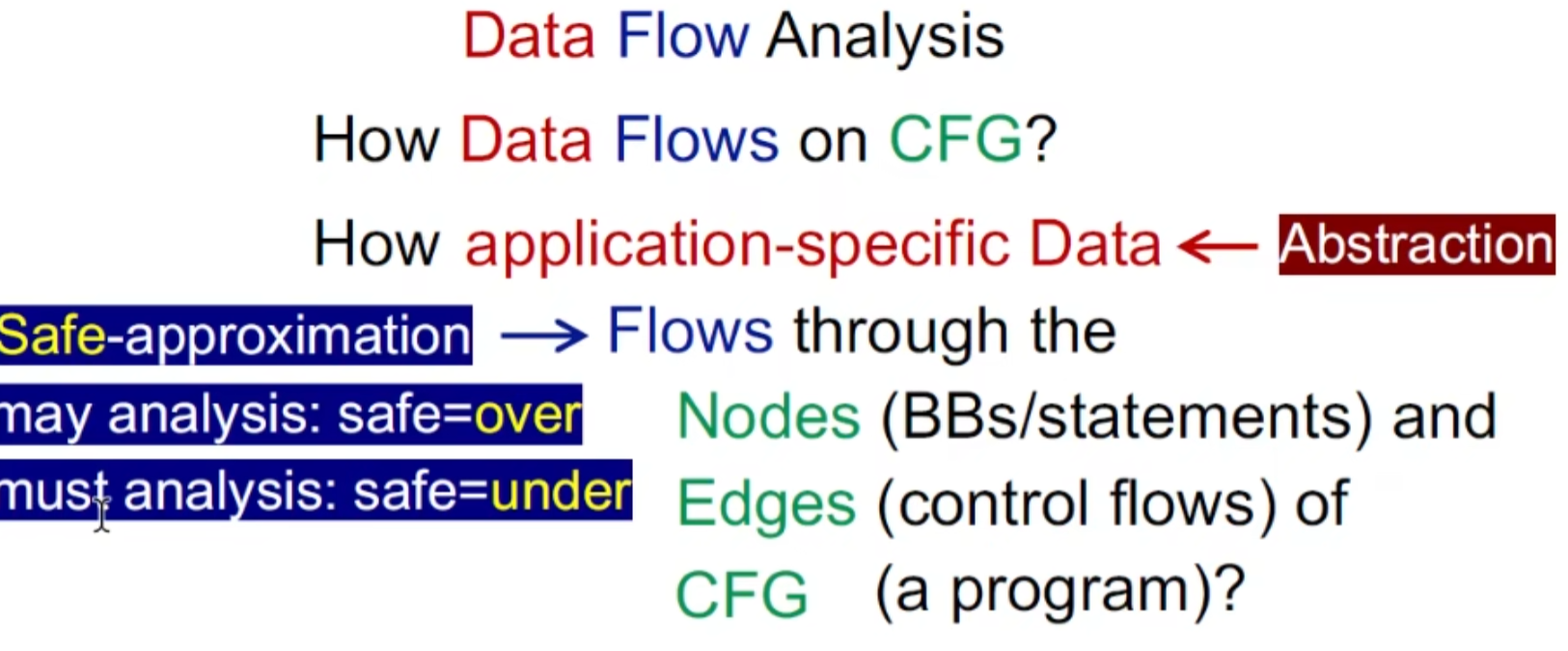
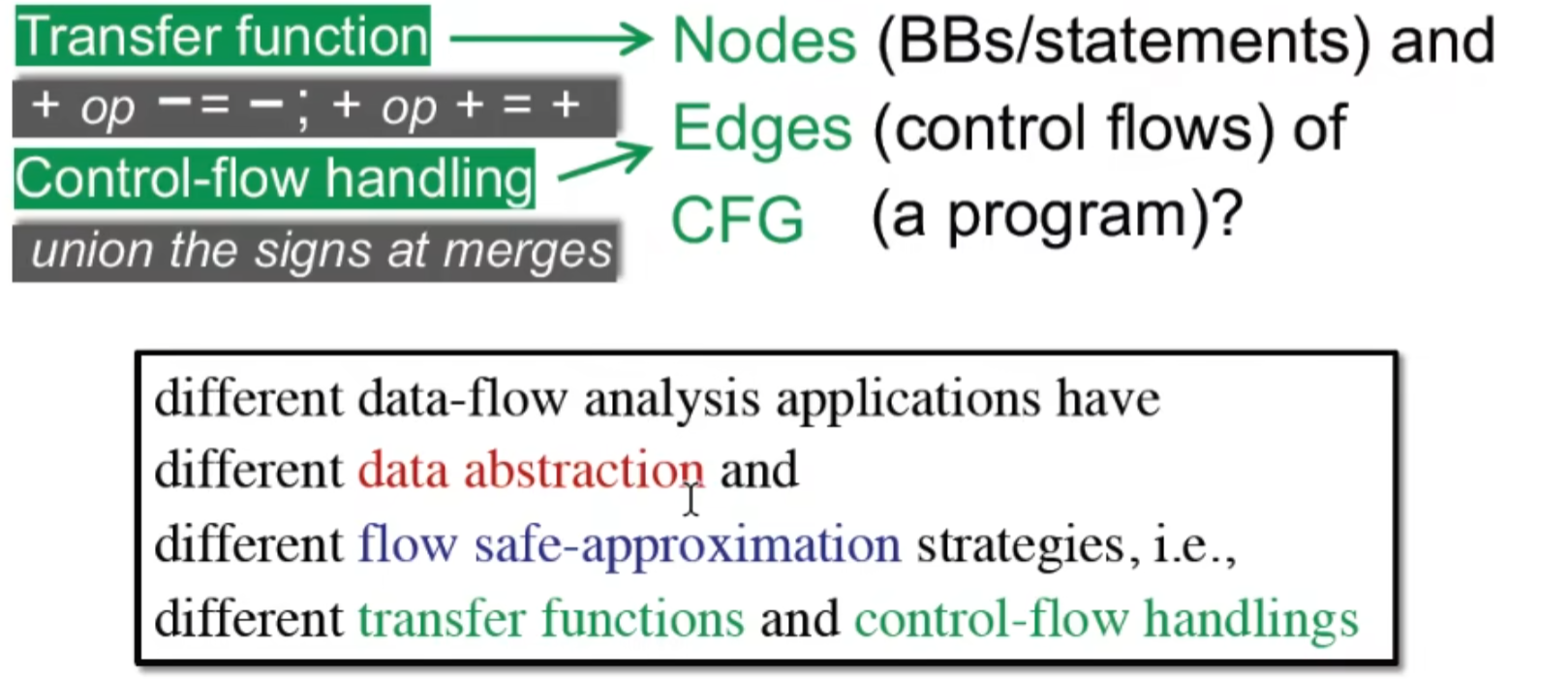
本质上是一种求解(?跟不动点有关)
主要就是处理 CFG(基本块之间),transfer function (基本块内)
一些基本的符号表示:
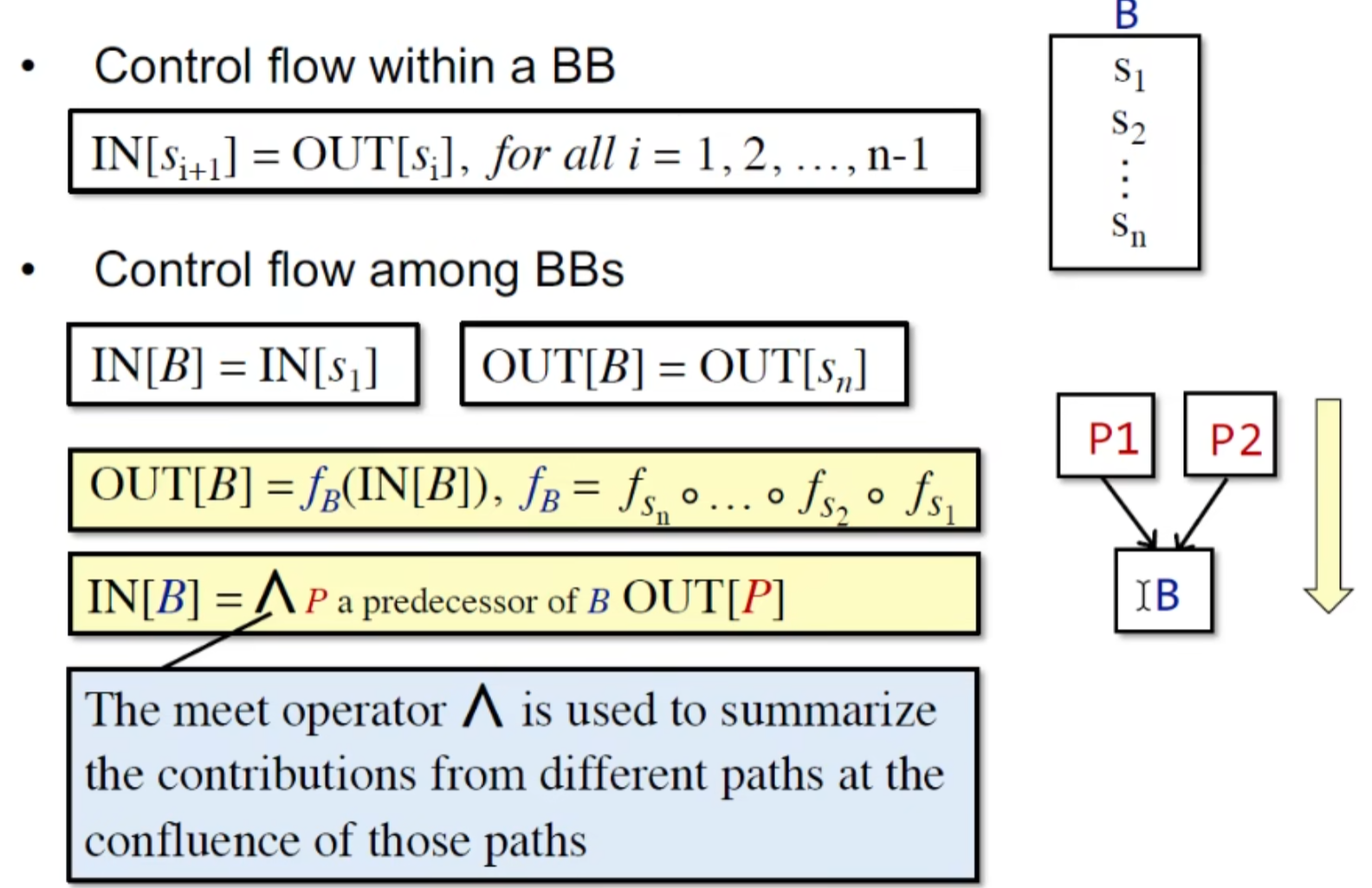
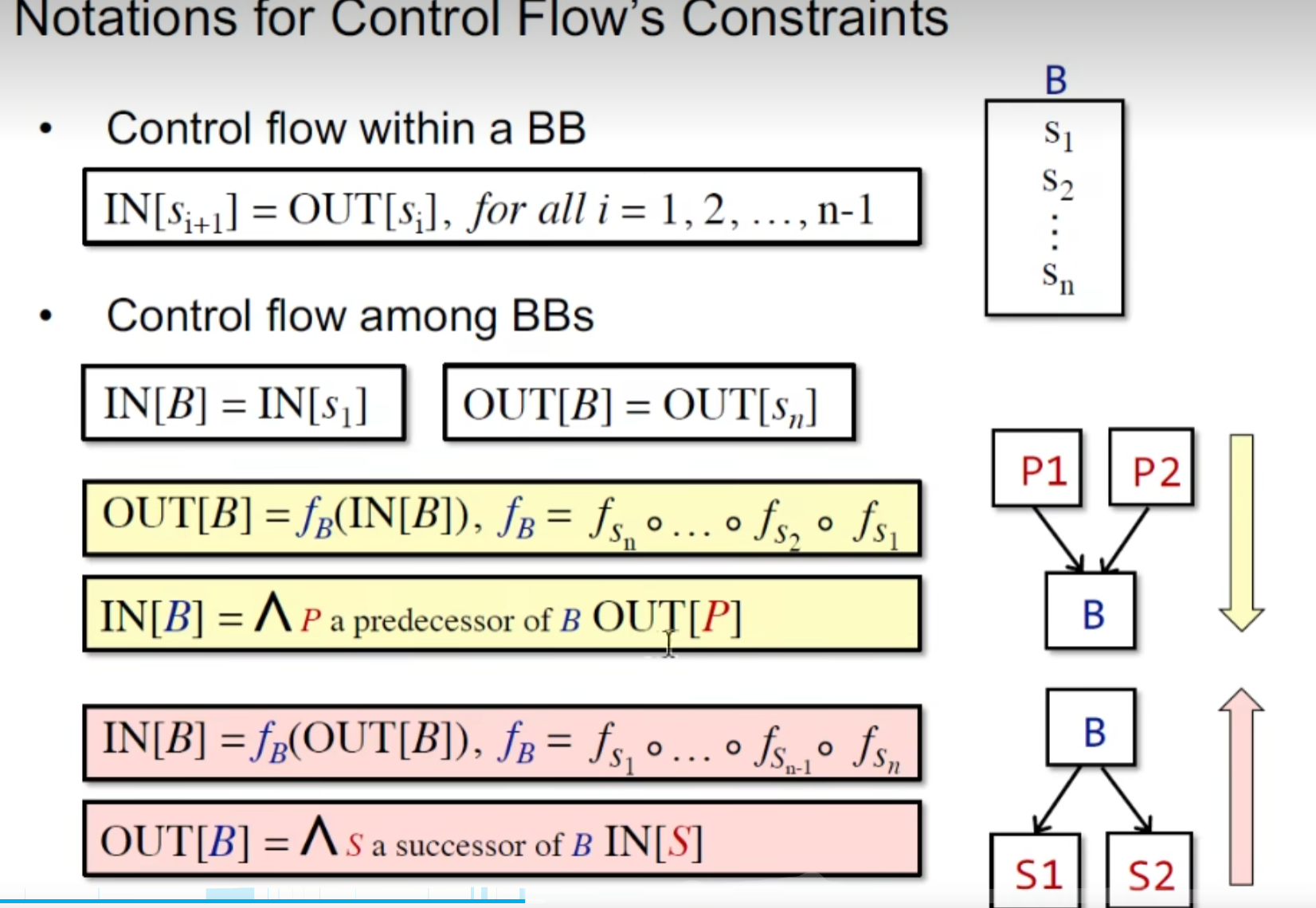
reaching definitions analysis
定义:

给变量v一个定义d(赋值),存在一条路径使得程序点p能够到达q,且在这个过程中不能改变v的赋值。
应用: 可以用于检测未定义变量

关注对象为所有被定义的变量,使用bitmaps 抽象每一个变量
CFG分析:
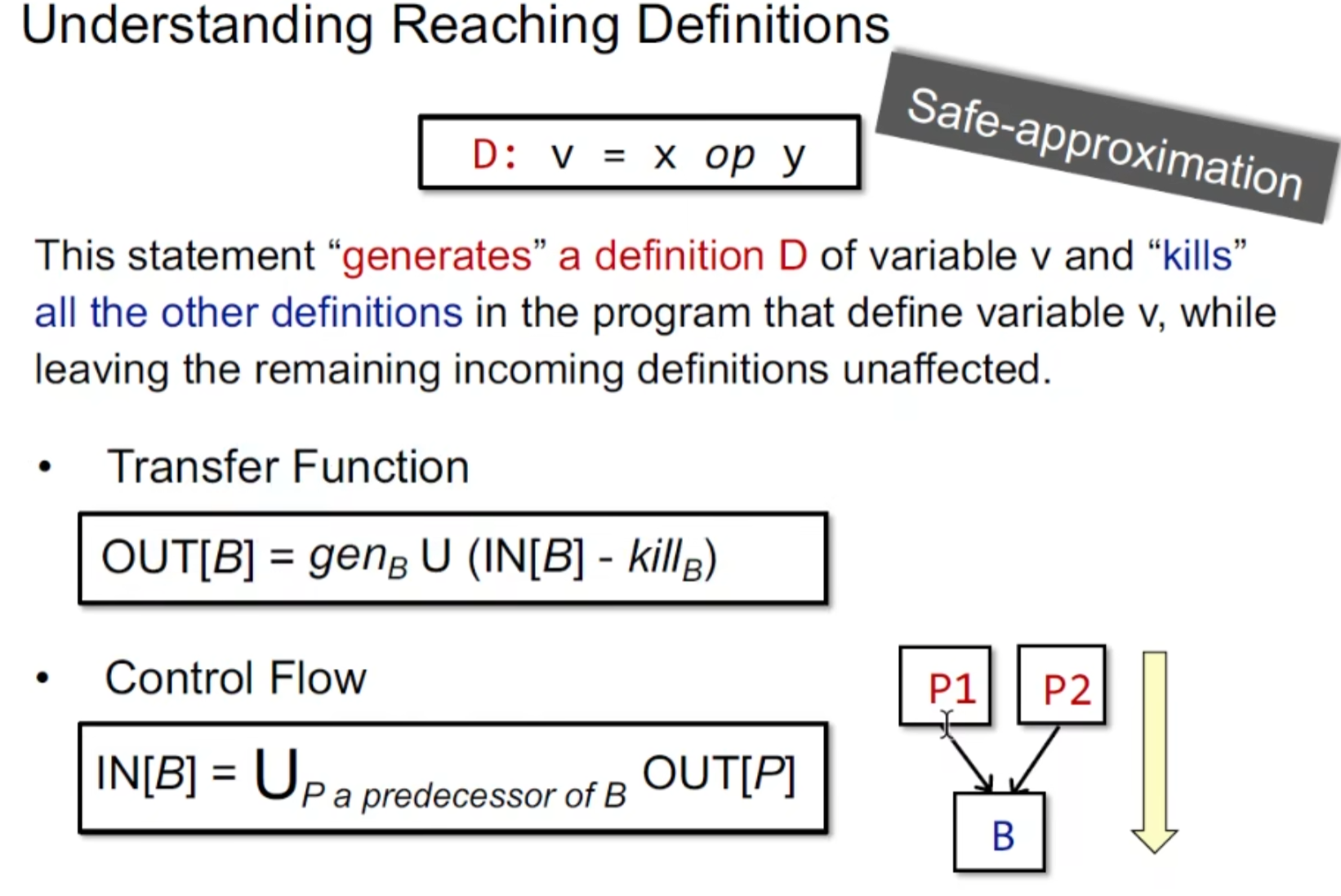
kill掉的是所有其他定义v的定义语句(也就是kill掉redefine)
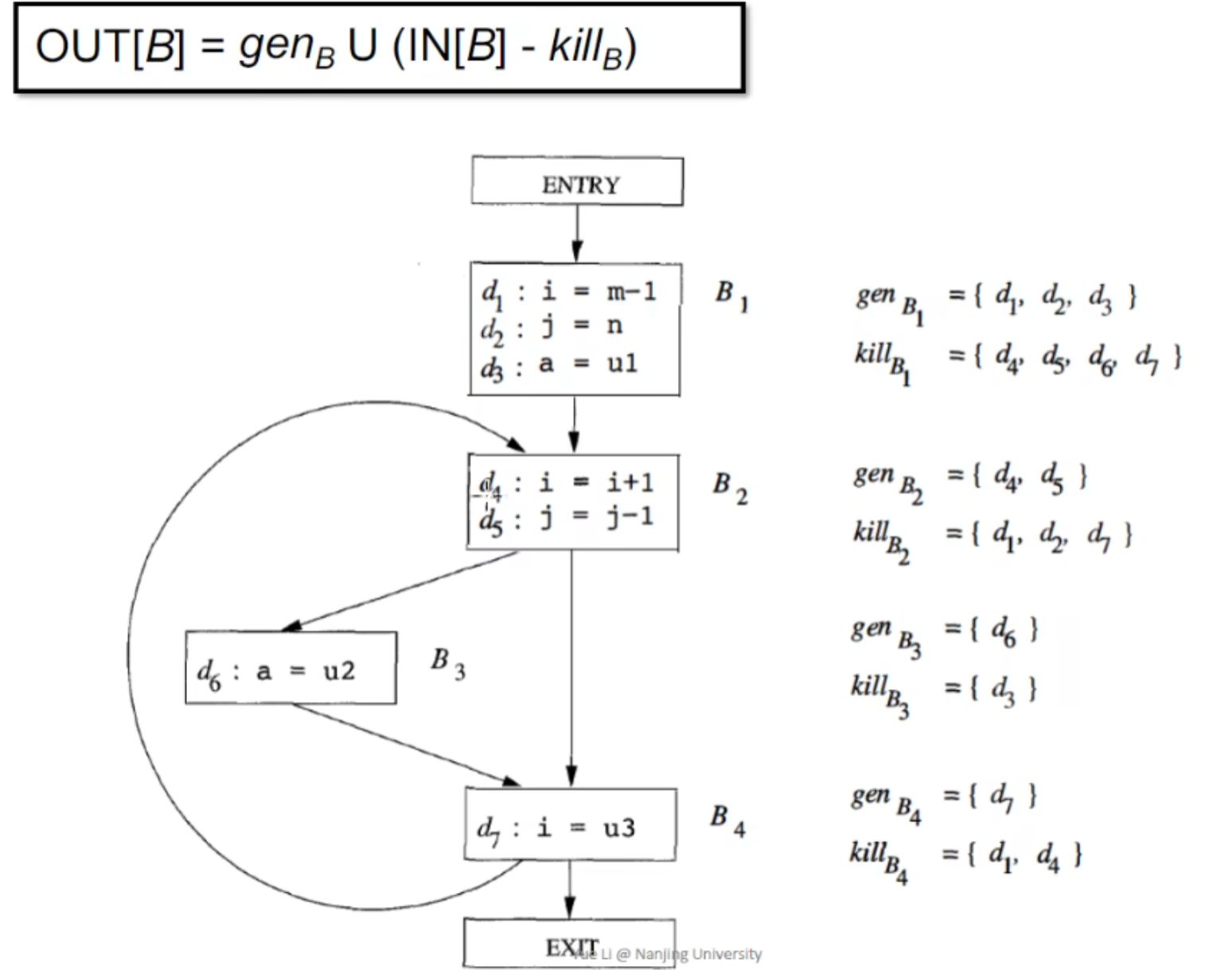
算法:

示例:
问题: 这个算法会停止吗?
OUT[B] = genB U (IN[B] - killB)
我理解为对这个集合求解 ,解出来的集合是有上/下界的 (全是0 / 1),而for循环内对out的计算又是单调的(不严格),out[b]至少是不会减少的,所以一定会有上界,算法一定会停止。
line variables analysis
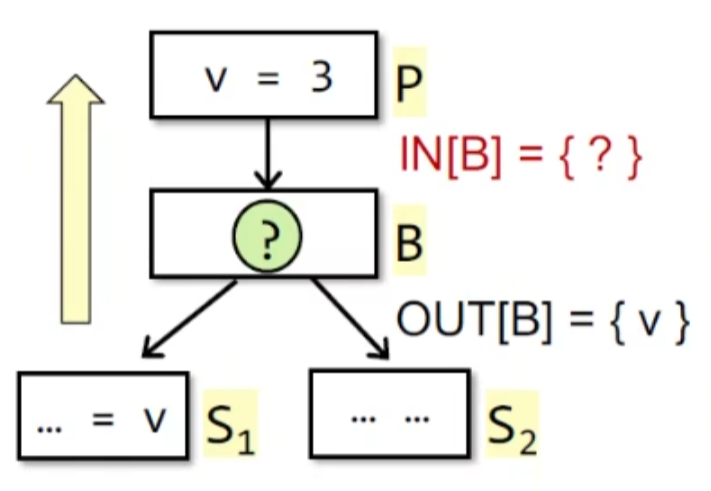
定义


简单来说就是分析路径中的变量值是否还存活,如上图所示,只要从p开始的某条路径中用到了变量v,则v在p处live。(变量v也不应该被重定义)
从定义就可以看出,这是一个may analysis ,因为是存在某条路径
运用场景: 编译优化 ,如变量替换寄存器时,选择一个dead的变量进行覆盖
运用backward analysis :这样更直观,只要从后面开始逆推的话就可以直接知道前面是否live了,如果使用forward,有可能得等到最后才能判断出一个变量是live的,此时又需要倒回去更新状态。
CFG分析:
由于是backward analysis ,故我们需要得出从out 到 in的表达式
通过六种语句分析:

情况4中,v是先被use 再 redefine的 ,本质上和情况6类似
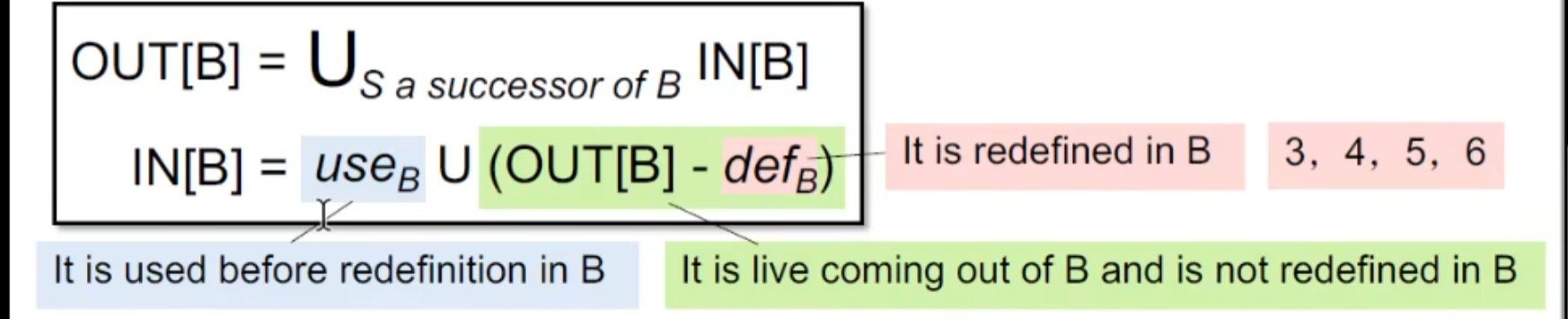
这里课件打错了,out[B] 后面那个应该是 IN【S】
1 | OUT[B] = US a_successor_of_BIN[S] |
被kill掉的情况其实就是 redefine (3,4,5,6) ,但要考虑 4 ,6 的情况 (在redefine之前被use) ,才得出这样的表达式,所以需要 注意 这里的use b并不是块中被use的所有变量,。
算法:
与Reaching Definitions Analysis 相似,区别基本就是换成了backwards

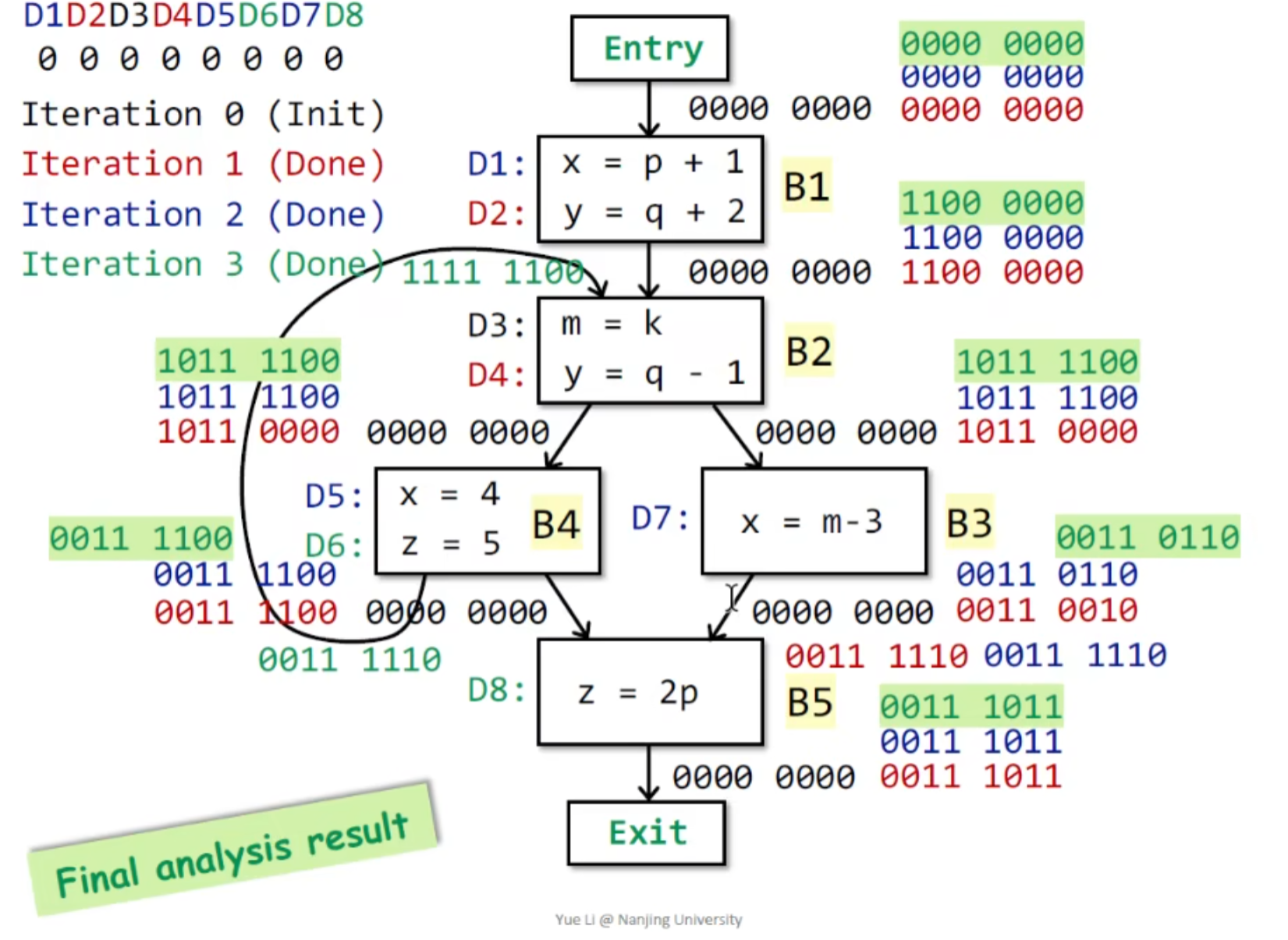
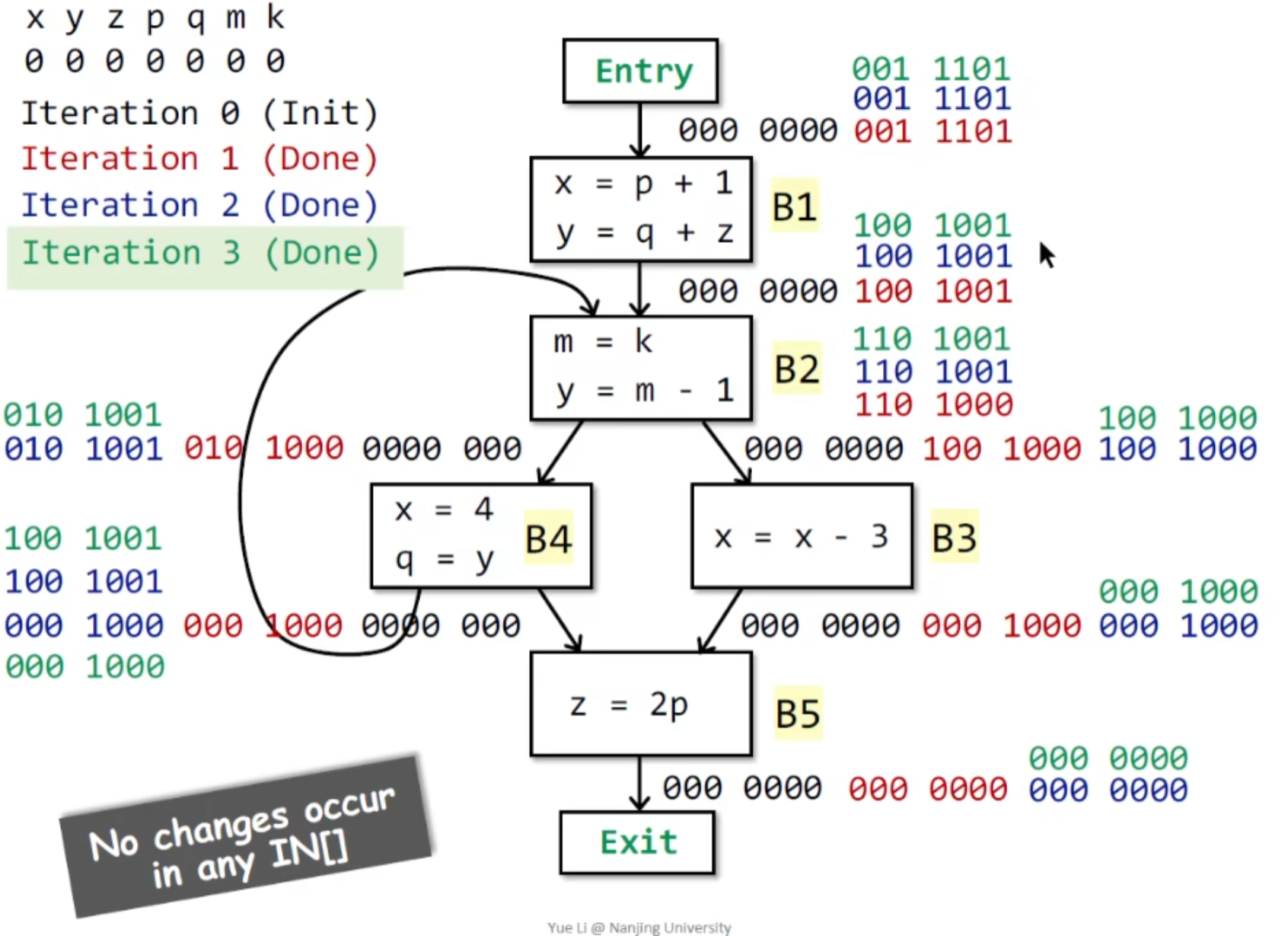
示例:
三次迭代以后, IN 不再改变
available expressions analysis
定义:

从定义可以看出这是个 must analysis, 需要全部路径都满足。
有点类似于表达式是否可以reach? 不是很直观,可以看一个available的例子:
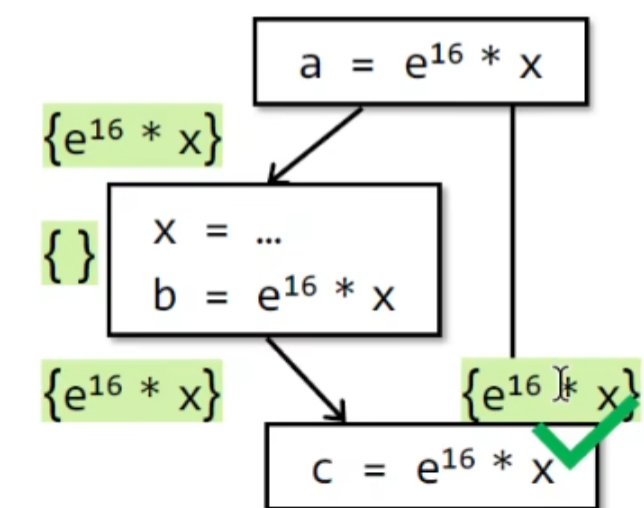
在此基础上我们可以做一些优化,比如说合并临时变量:
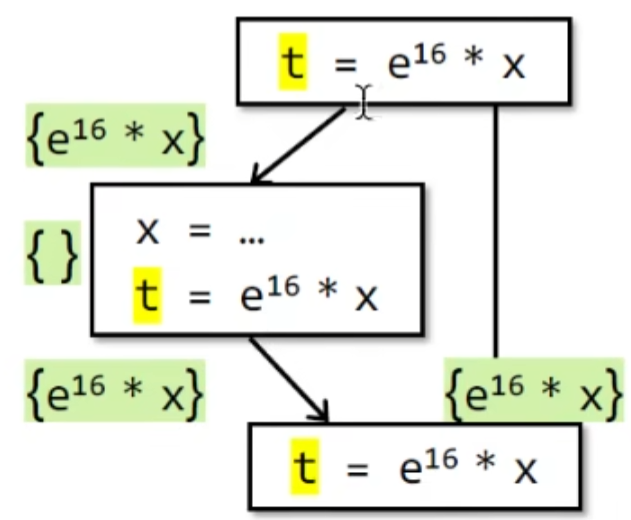
在这个例子中 ,我们不需要考虑中间的path,直接计算t的最后一次expressions即可得到t的值
与前面对象为变量不同,分析对象为全部表达式

CFG分析:
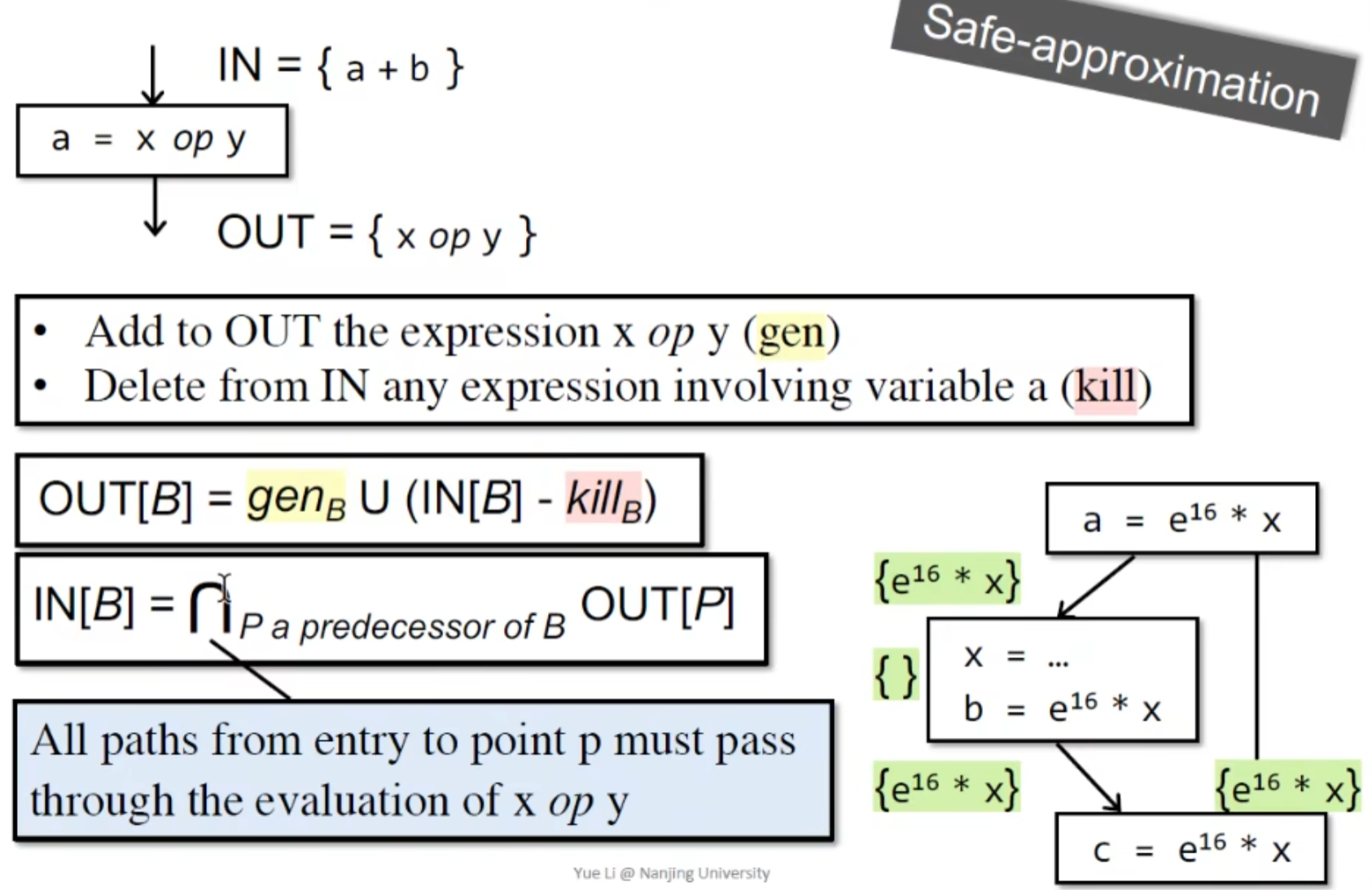
genB为块B中所有的新表达式,kill去变量被redefine的表达式
IN[B] 取交集,也就是满足 all path
我们需要safe- approximation,就算我们有漏报(本应是available 报为unavailable ),也算是safe的,最需要保证的是不要优化错了(误报),也就是must analysis -> under-approximation

算法:

计算的时候 先计算kill B,在计算gen B,可以解决表达式中一个变量被重新赋值,但该表达式又被再次使用的情况,或者直接按statement的顺序一句句计算也行。
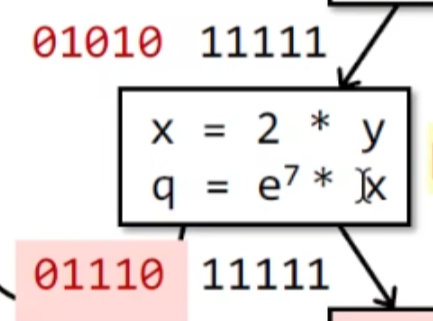
示例:
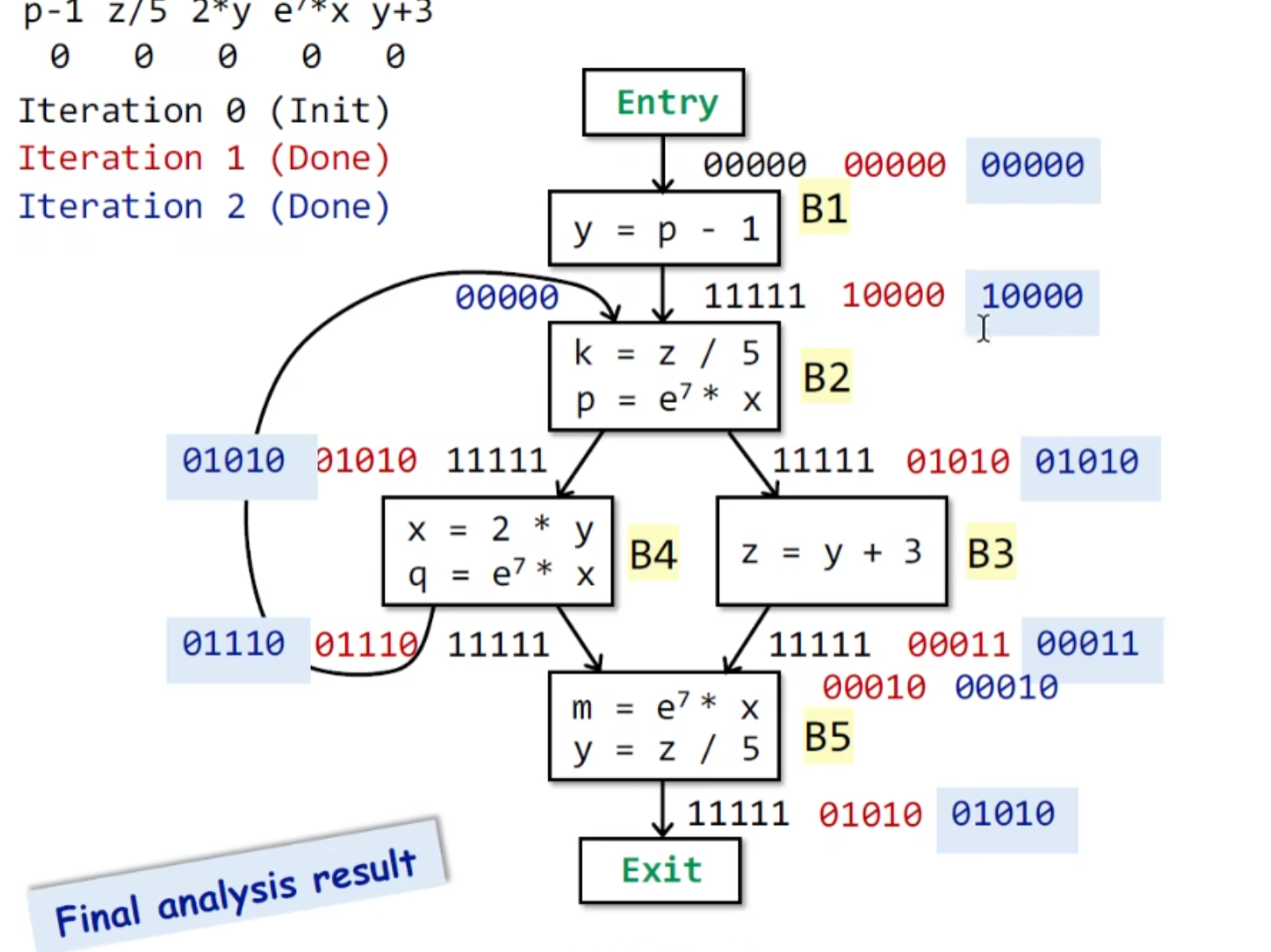
comparison
Boundary与 Direction 有关,forward的话就是entry,backwards的话就是exit
Initialization 初始化值与may/must 有关, 对象与Direction有关(参考Bondary),may常常初始化为空集,must常常初始化为全集。
must 通常为 ∩ ,也就是汇聚,may通常为 U,这里我也不是特别理解(我就简单理解为,may是某条路径的话自然取交集,must同理自然取并集 ),老师也没讲理论还
Foundation
这里涉及到很多集合论相关的,我只在离散数学中接触过一些
函数和集合
V k 代表一个 k个节点的CFG的 OUT的集合

函数可以看成集合到集合的一次迭代
非常直观的解释,引入不动点,我们前面的dataflow analysis,本质上也是找到函数的不动点

问题:
- 算法一定能找到不动点吗,该函数一定有解吗? 涉及单调性
- 如果存在解,那有多少个解(不动点)?
- 我们的算法需要多少次迭代才能找到不动点?
偏序集
离散数学学过一些,简单截个图
主要就是讲 偏序关系 的 自反性,对称性,以及传递性,

偏序关系不要求任意两个元素都满足偏序关系

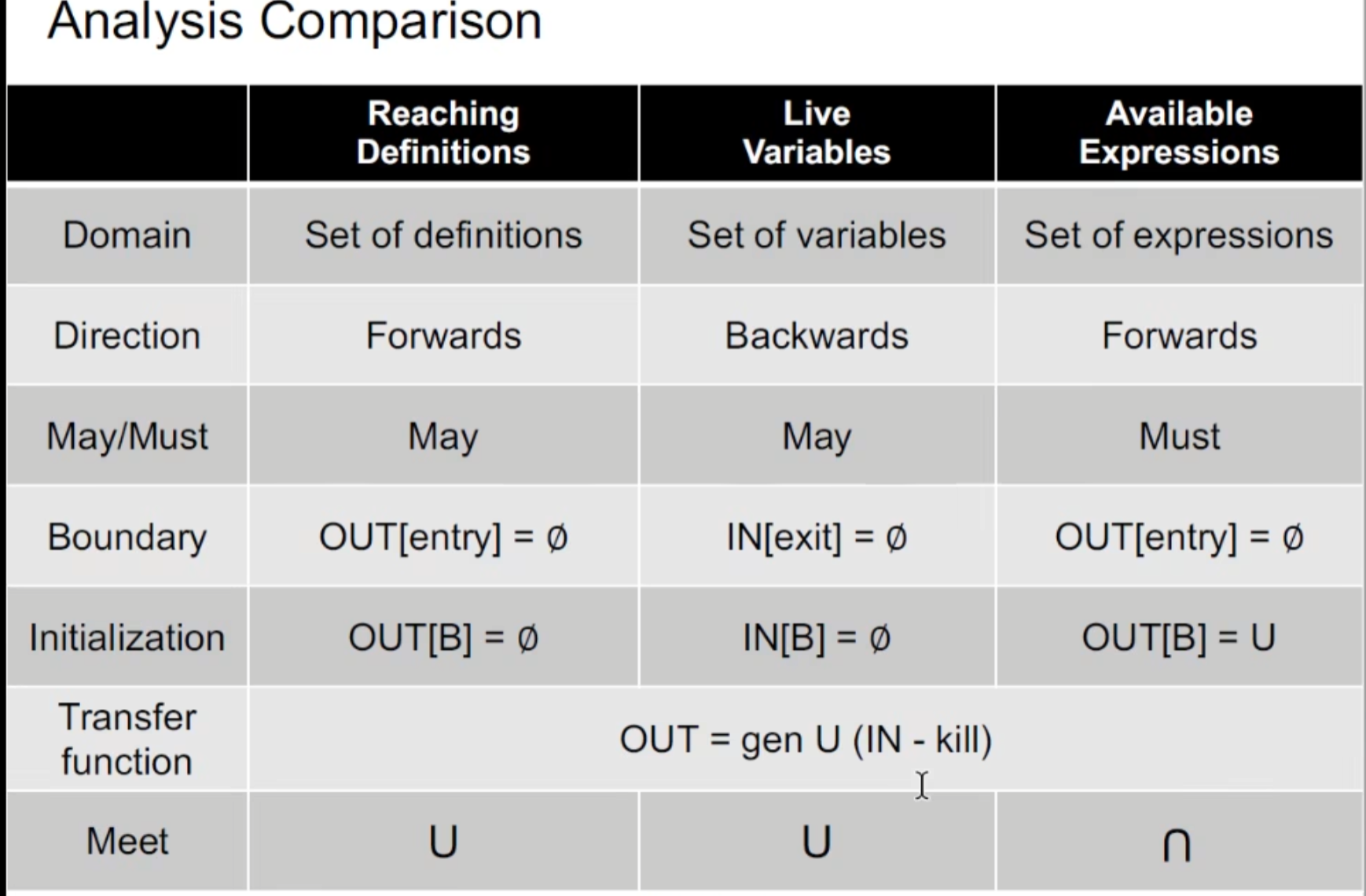
上下界 最小上界 最大下界
主要认认符号
需要注意的是 子集的上下界并不一定属于该子集 ,注意看上下界的定义就是了。
最小上界(lub / join )
最大下界 (glb / meet)

清晰的例子:
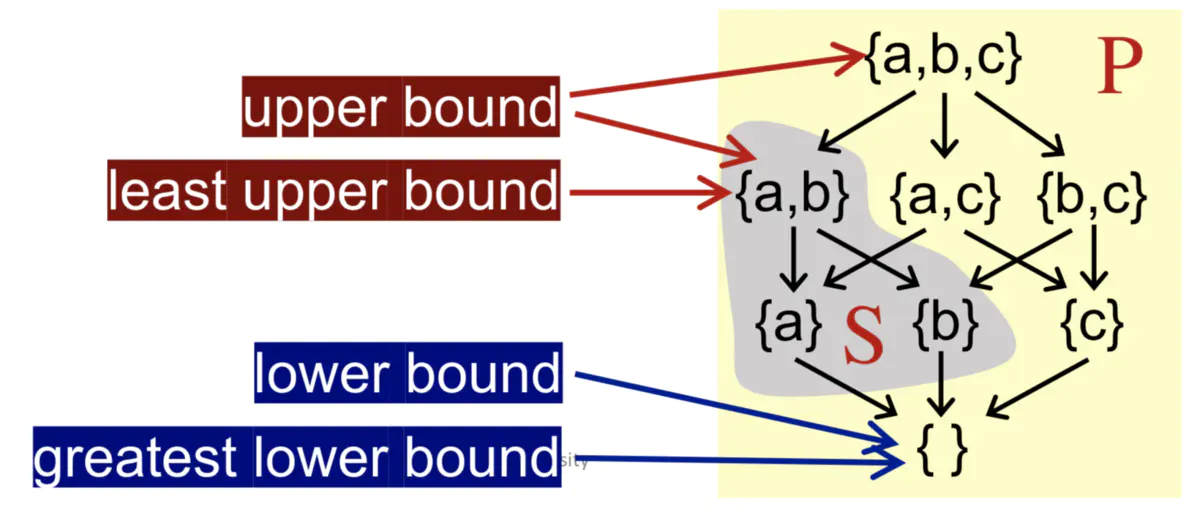
性质:
- 不是所有偏序集合都有 最小上界 / 最大下界
- 如果存在 最小上界 / 最大下界 ,那它一定是唯一的
证明很简单,离散上也讲过,这里给出反证法
格( lattice)/ 半格 / 全格 / 格点积
格:偏序集中的任意两个元素构成的集合均存在最小上界和最大下界
半格: 偏序集中的任意两个元素构成的集合均仅最小上界或最大下界存在
全格: 偏序集中的任意若干元素构成的集合均存在最小上界和最大下界 (全格的任意子集都满足格)

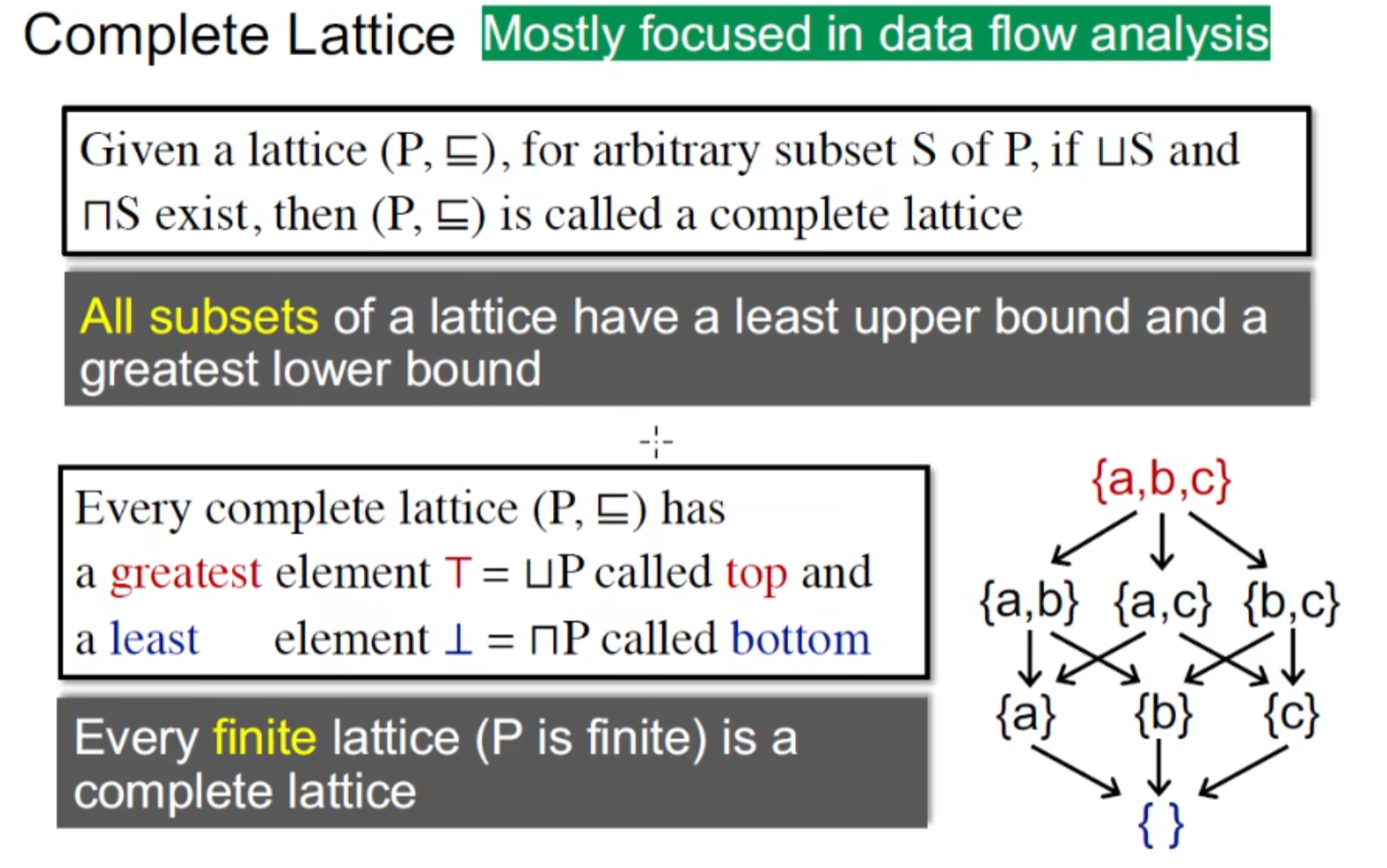
complete lattice为我们主要关注的,我们静态分析的对象一般是有穷的全格
还有就是记住top 和 bottom
Product Lattice(格点积)

上面的 ✖ 是笛卡尔积
- 格点积是格
- 若构成格点积的格是全格,则 格点积也是全格
通过 格 表示 Data Flow Analysis Framework (D,L,F)
- D代表CFG方向,forward/backwards
- L代表格 ,值域为V ,join 或 meet 操作(偏序关系) (CFG 块间操作)
- F代表transfer functions,集合V->V 的迭代 (块内操作)
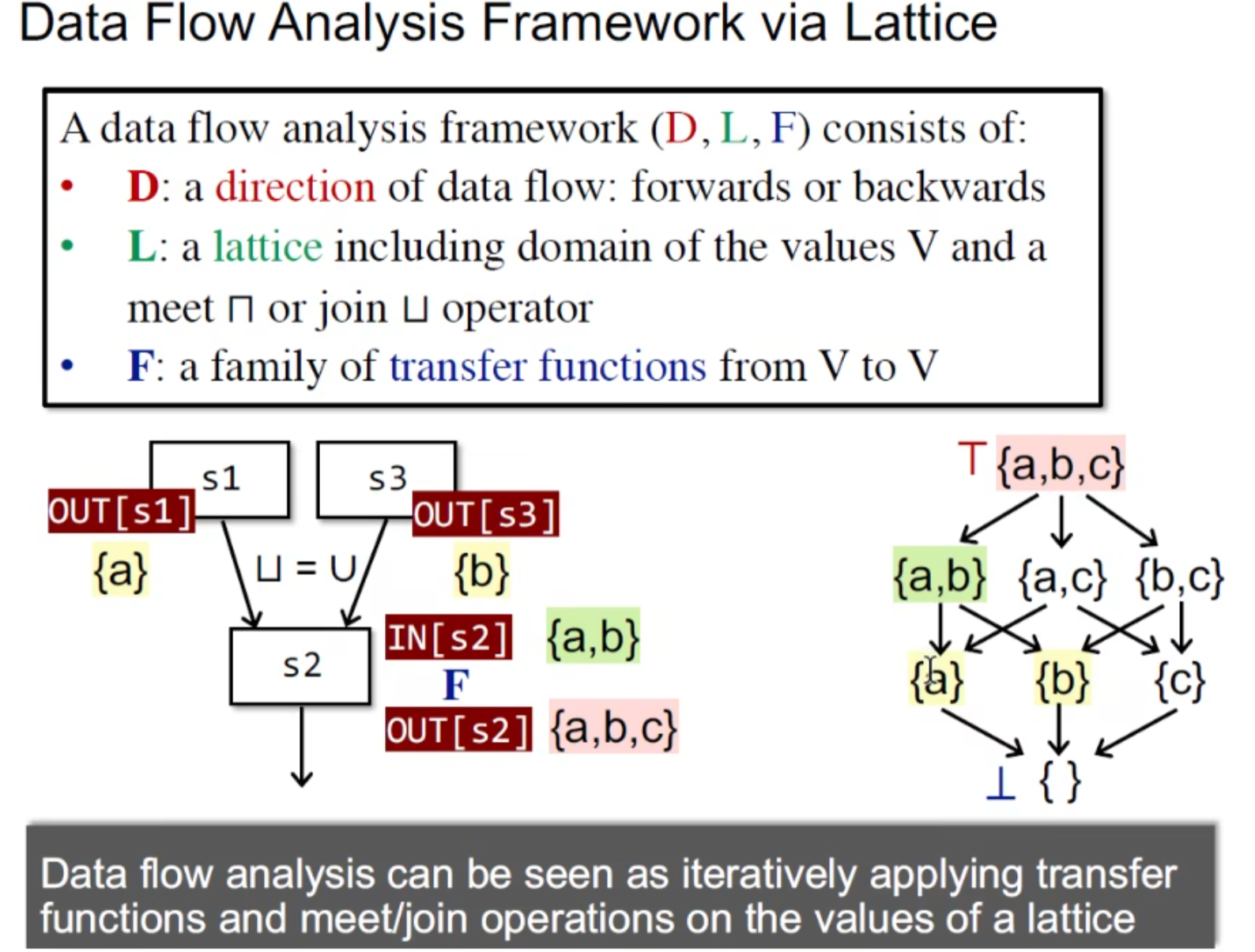
那么Data flow就可以看成是通过 对格进行 join/meet 以及 F 操作
不动点定理
单调有穷的格 ,对 top / bottom 迭代可以得到最大不动点/ 最小不动点

证明:
证明存在不动点 存在
以bottom为例

有点像鸽笼原理,L的值域优先,假设有k个元素,在k+1 次迭代中 必然会存在两个相同的值
不过这里用鸽笼原理,是k 和 k+1 就说不通了,应该结合了单调性 ,比较trick
证明最大/最小不动点
假设了有别的不动点,证明我们求出的不动点一定小于等于别的不动点
此处用了数学归纳法

证明唯一:
参考最小上界/最大下界 唯一的证明,基本类似。(利用反对称性)
add /edit stuck
迭代算法不动点证明
首先需要证明我们的迭代算法对象是 一个 单调 ,有穷 的 全格
全格证明:
通过product lattice 证明 ,每个BB的值域相当于一个lattice,每次迭代k个BB的值域就是k-tuple,k-tuple 可以看成是lattice 积,根据格点积性质即可证明为全格。

有穷证明:
我们的集合是有限的(不然我们求个无穷解干嘛),值域就是 0 / 1 ,所以lattice有穷
单调证明:
首先,Gen / Kill 表达式 是单调的(不严格),这在前面的3个analysis例子就可以直观看出来了
现在主要证明 二元操作符是单调的 ,二元操作符就是我们块间操作时的meet/join
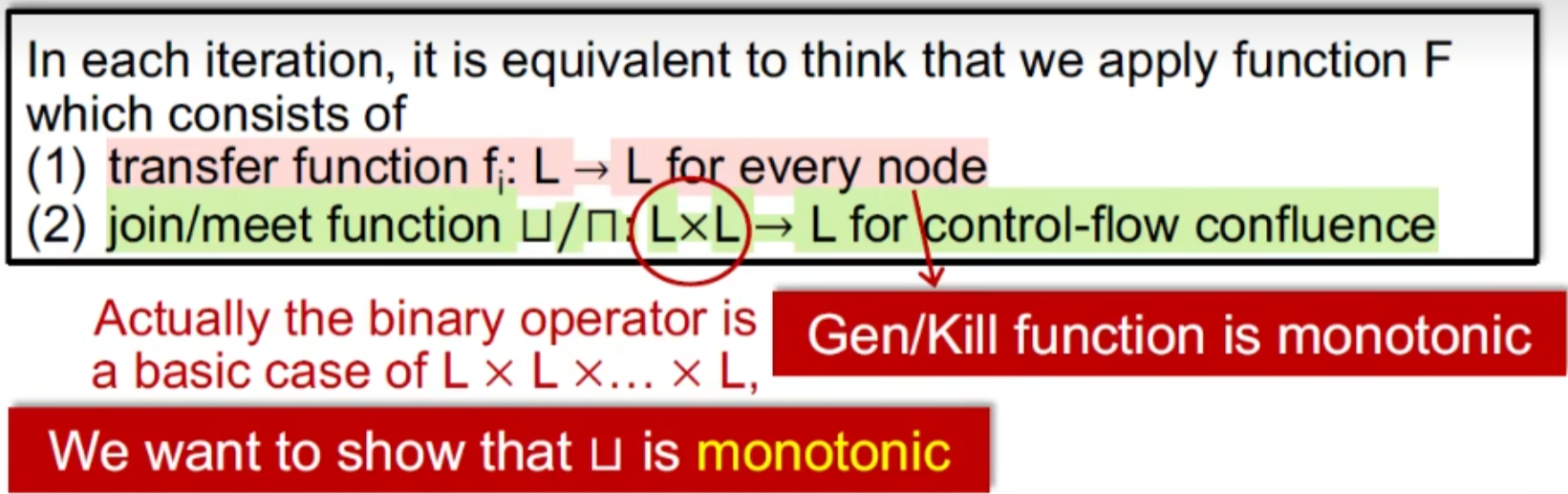
用上下界和偏序集的性质证明:

现在回到前面的第三个问题:
什么时候会达到不动点
lattice高度定义:

考虑最坏的情况,每次只有一位变成 0/ 1 ,那每次都会走h步,走k次,那就是h*k

三个问题基本解决:

may/must analysis分析
我们把整个BB构成的CFG看成一个product lattice ,这样可以就是对一个lattice
无论是may/must analysis ,都是从unsafe->safe 走,且是单调的
以reaching definition来看 may analysis
从unsafe result出发 ,初值为bottom(没有define可以reach) ,直到第一个不动点(最小不动点),得到一个safe result,这是一个best的不动点,因为越靠近Safe 越没用(比如说直接假设所有变量都有可能reaching,虽然safe,但是没几把用)
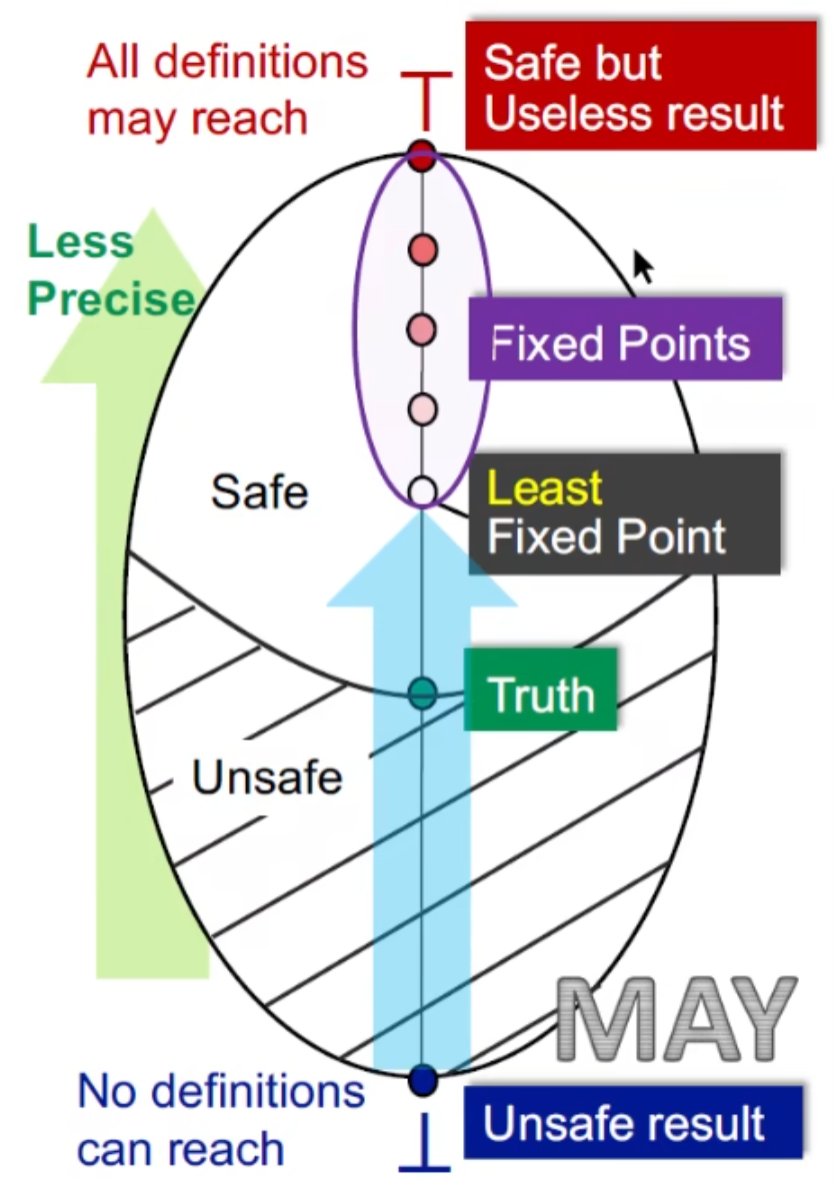
以 available expression 来看 must analysis
需要从unsafe的结果出发,初值为 top(所有expression都available,可以被优化),最终会走到最大不动点,这也是一个best的结果。
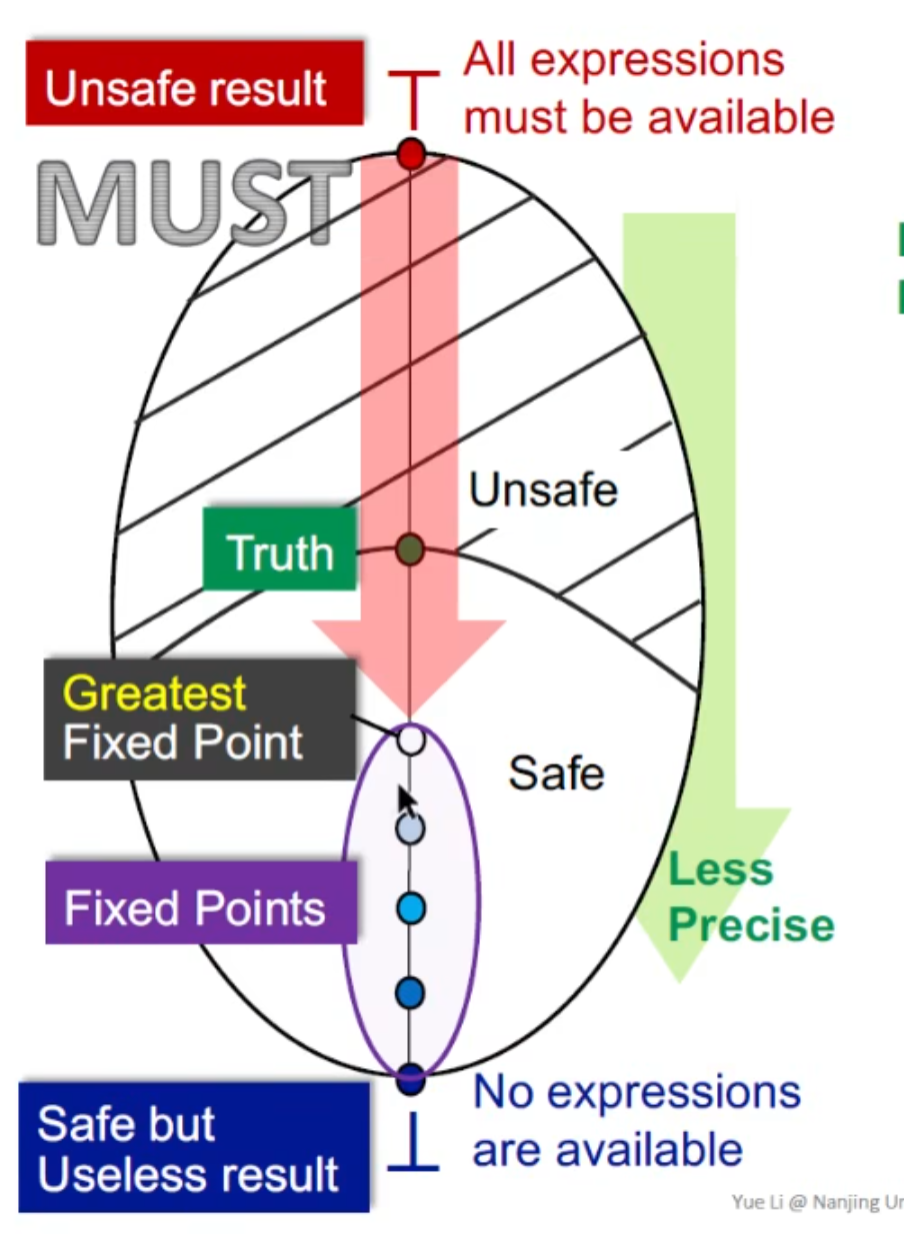
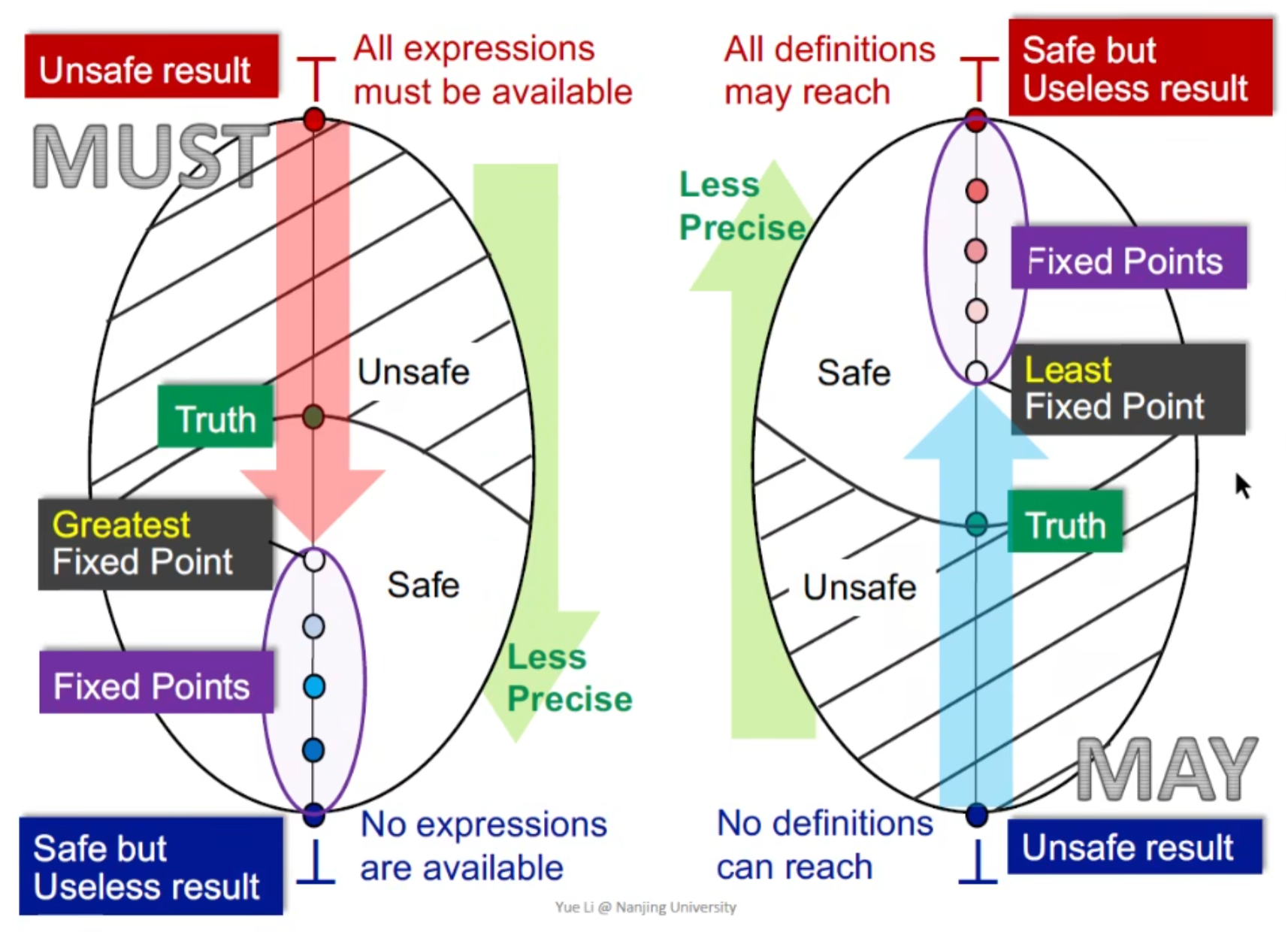
这样就解决了我们前面第二个问题,求出的不动点为什么是best result
另一个角度:
may analysis时使用union ∪,而must analysis使用 ∩
衡量精度 MOP
MOP(Meet-Over-All-Paths Solution)
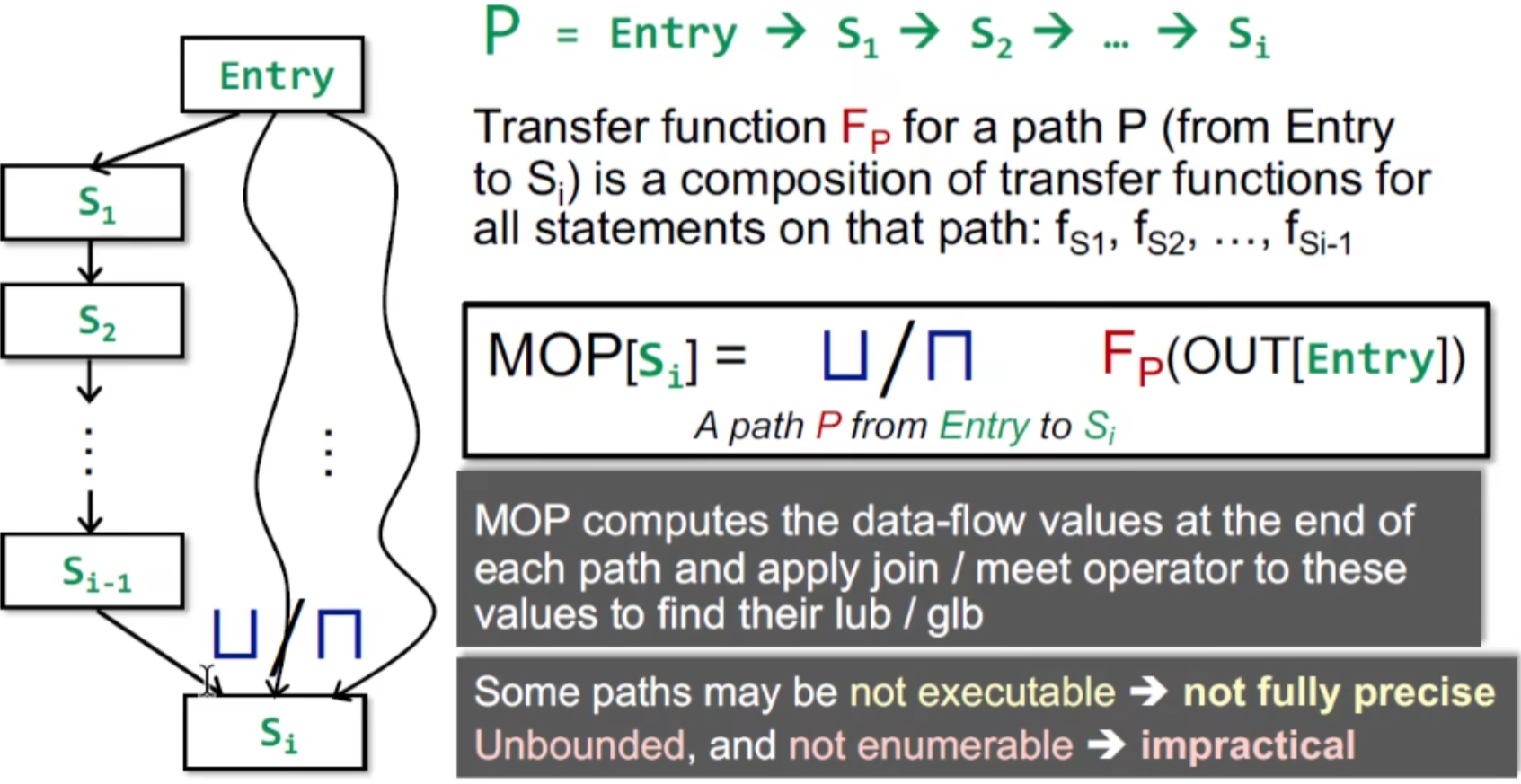
有循环的话很容易路径爆炸
迭代算法 VS MOP
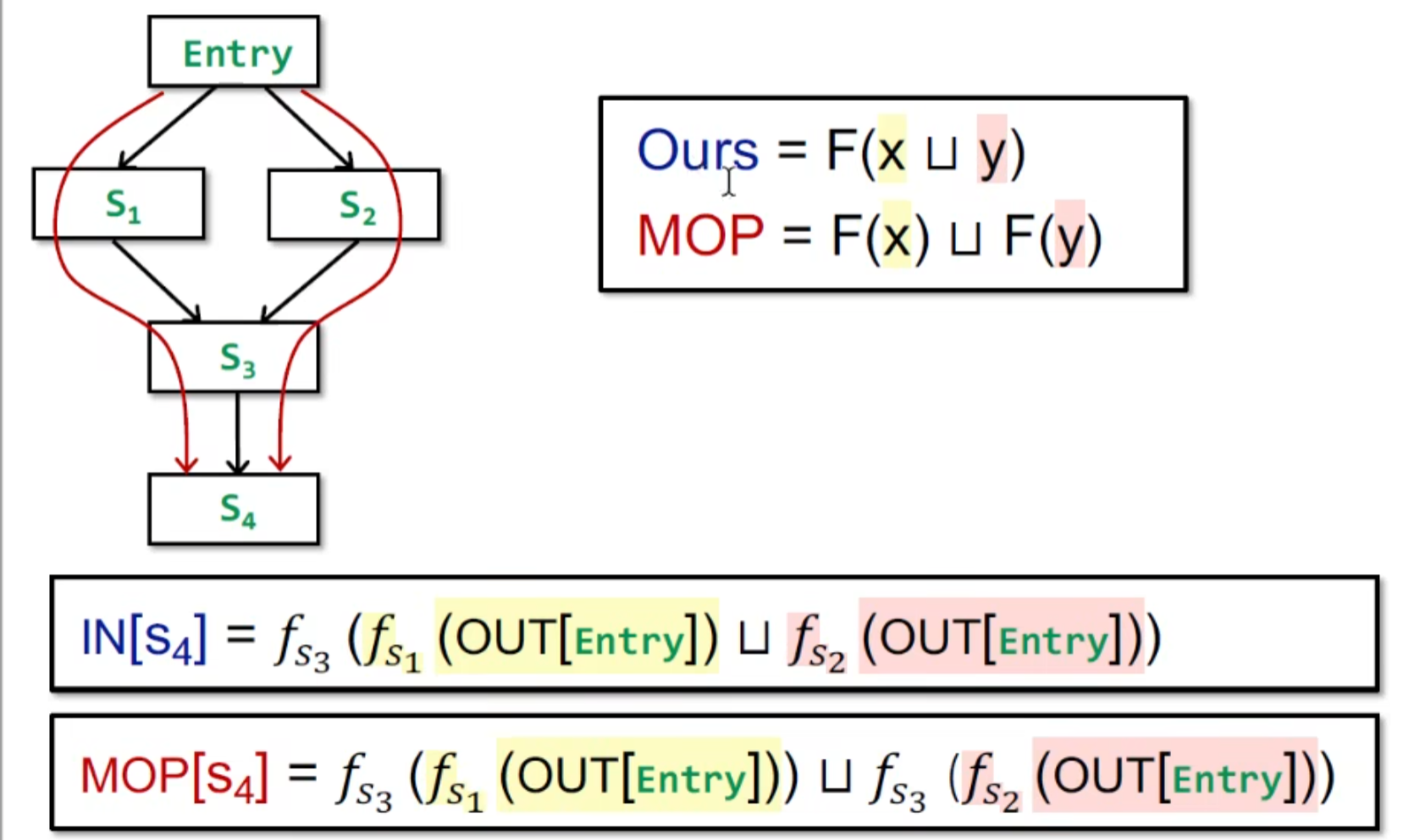
MOP会比我们的迭代算法更准确,证明:

当然 ,这是偏序关系,如果F运算满足分配律,那他们可以是相当的

constant propagation 常量传播
涉及lab1,不过我可能不一定有机会来做lab?
判断p处变量x是否为常量,(x,v) 表示变量x可以由常量v代替
D: forwards
L:因为要考虑所有的路径,x在所有路径值都不变才为常量,故为must分析,must的unsafe->safe,就是以所有变量都为常量出发(这样做优化就是unsafe的,相反如果认为所有都不是常量,不优化就没影响)
变量初始化为常量不好表示,在初始化前都是undefine,所以以undefine来初始化表示
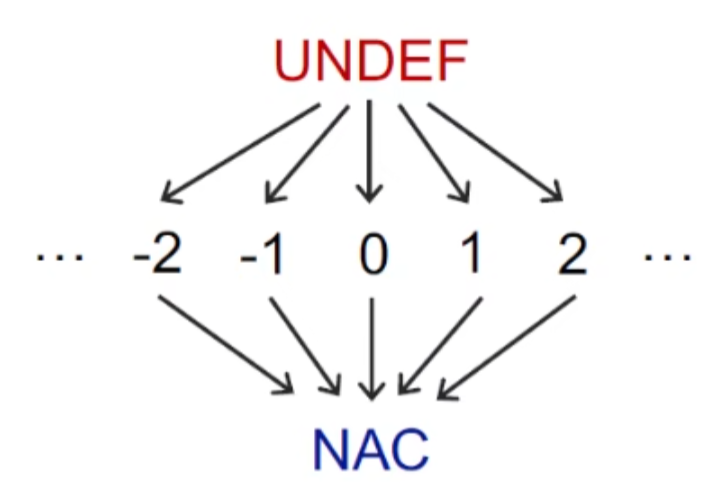
meet/join,我们在每个路径的汇聚处都进行meet operation,这里的meet操作为我们自定义的

这里有一点就是如果有一条path是undefine,其他path都是常量v,那么我们也认为x是常量,是正确的
F: val() 为取对应变量的值
对于新加入的语句,主要有常量赋值,变量赋值,表达式赋值三种,分类处理
这里有一个trick,对于y,z一个是undefine,另一个是constants的情况,y op z也算作undefine,否则的话整个f表达式就不满足monotonic了。
如果算作是constants,整个lattice就可能存在往回流的路径了(参考前面的图)

是否满足分配律?
考虑相加为常量的情况,可以看出是不满足的,也就是精度不如MOP

迭代算法优化 worklist
原算法:

while循环的冗余了,我们前面已经知道,我们只需要重新计算out改变的nodes即可,不需要所有的nodes都重新计算。
采用队列进行存储,初始化为所有nodes
因为前驱的out不变的话,后继的in就不变,只有前驱的out变时,才需要把所有的后继加入worklist
故每次循环判断当前的nodes out是否改变即可。

Interprocedural Analysis 过程间分析/函数间分析
原因:
我们以往的过程内分析只考虑了过程内部的语句而忽略了过程的调用,这会导致我们分析不精确。
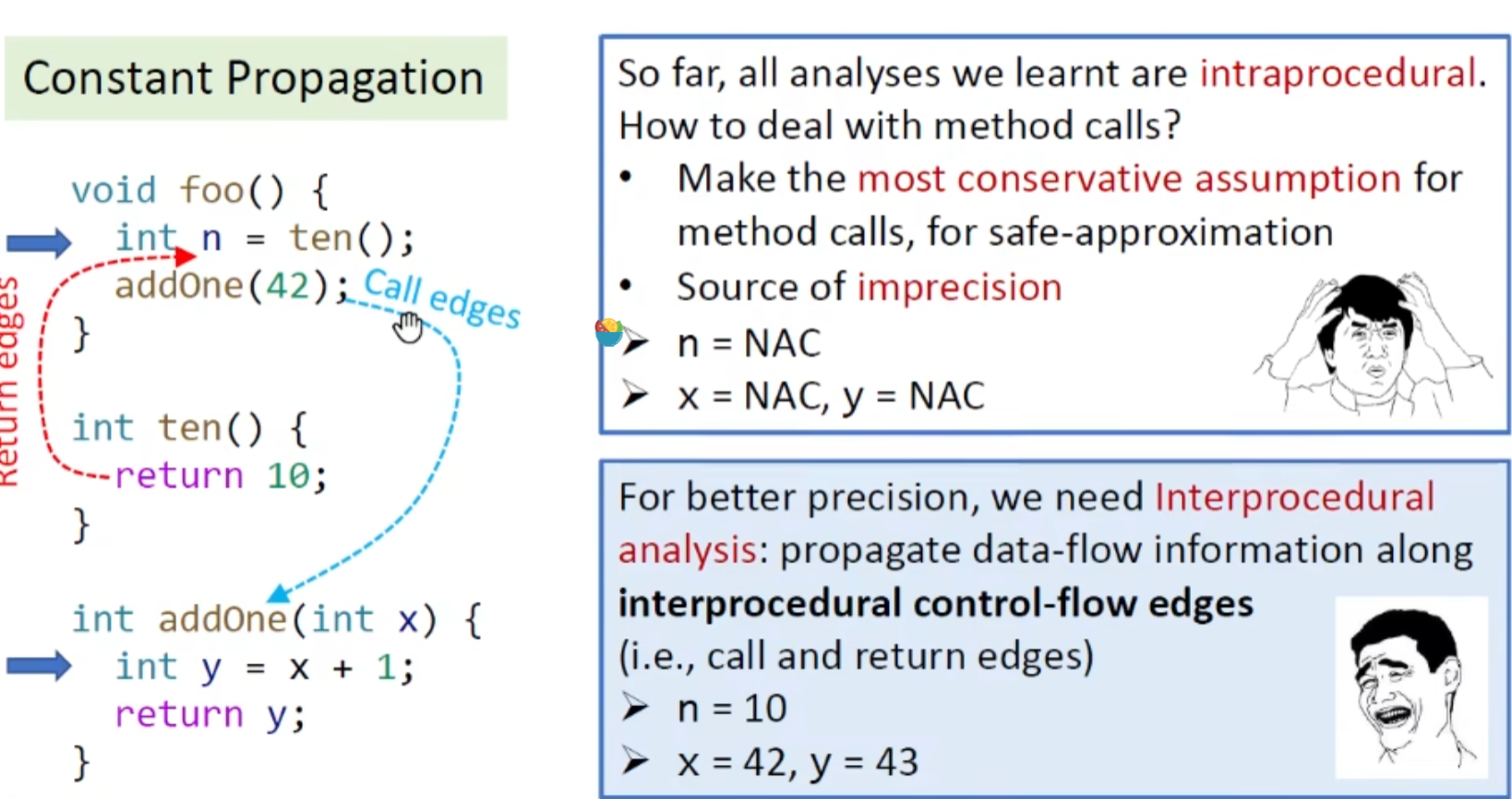
Call Graph
为了实现过程间分析,我们就需要知道调用关系,绘制出程序的调用图 call graph
简单来说就是调用点(call sites)到目标方法(target methods)的**边(edges)**的集合
一个简单的例子:
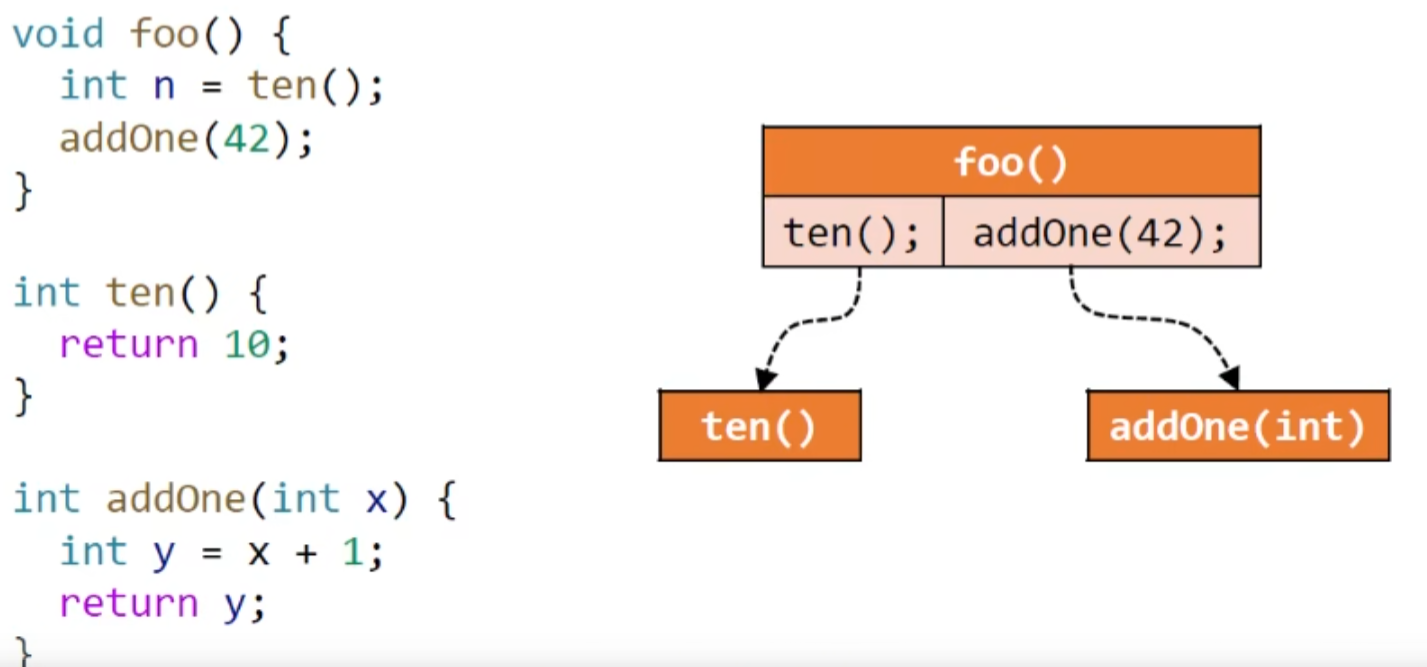
call graph的应用
- 理论上过程间分析(跨函数分析)的基础,
- 程序优化
- 程序理解
- 程序调试
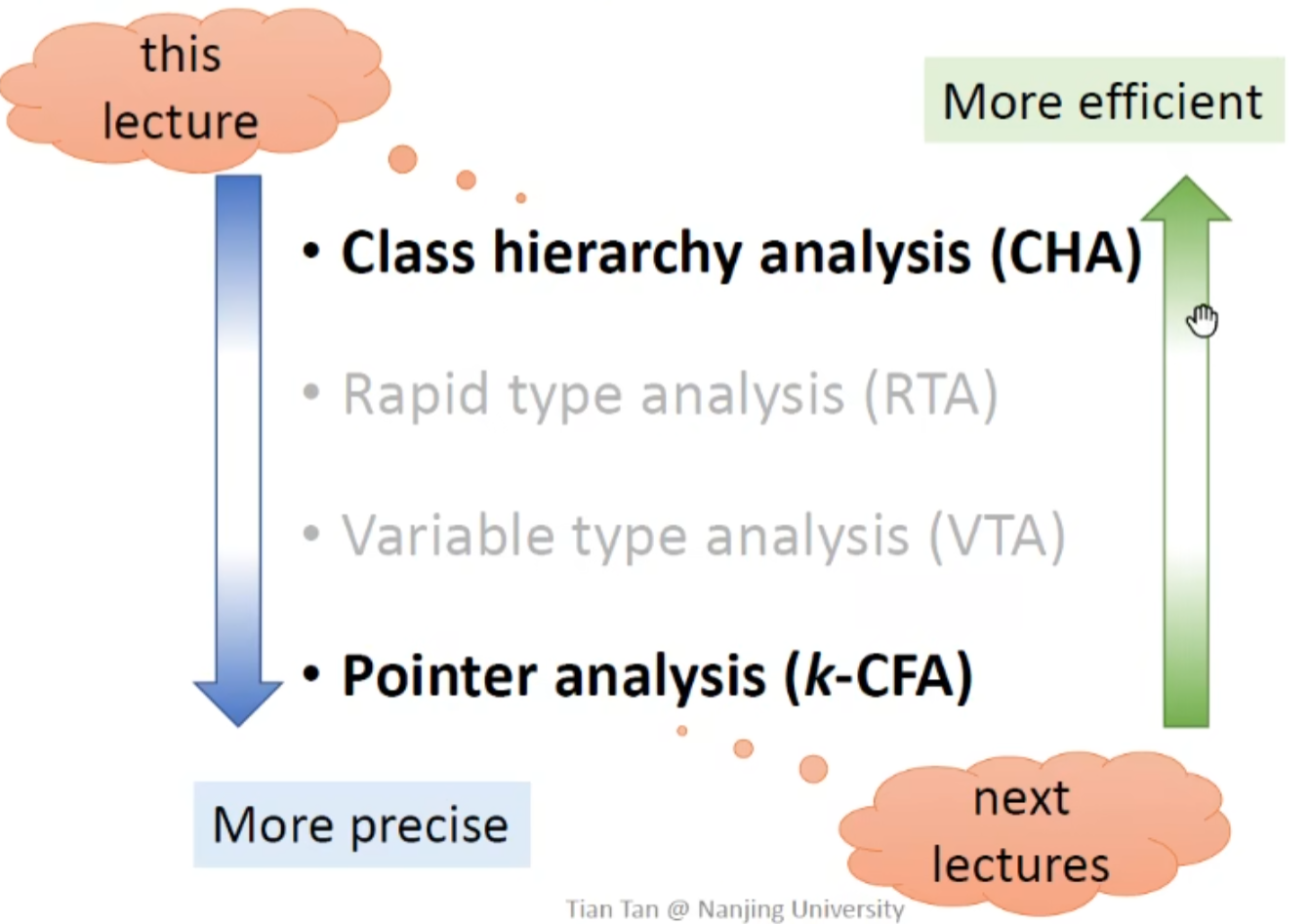
面向对象的call graph构造 (Java 为例)
我们分析第1,4个算法(CHA,k-CFA)
方法调用分类,主要三种:静态调用,特殊调用,虚函数调用
virtual call无法在编译时决定目标函数,我们主要的关键就是处理virtual call,另外两个都只有一个目标函数,相对来说简单一些。
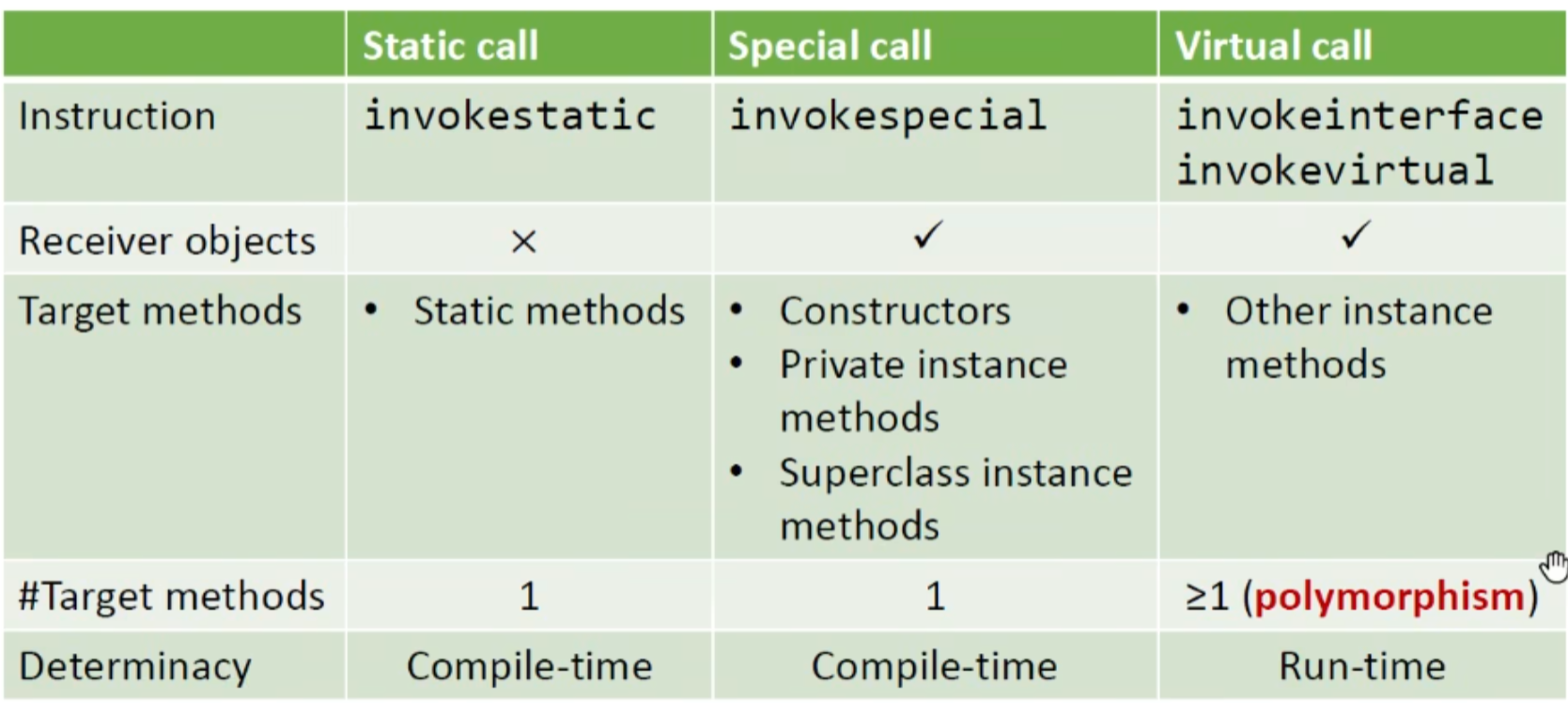
method dispath of virtual calls
virtual call 需要运行时才能确定,主要涉及两点:
接受对象的类型 c
call site 处的函数签名 m

函数签名:
signature = class type(类名) + method name(函数名) + descriptor(描述符)
descriptor = return type(返回类型) + parameter types(参数类型)
下图右边为soot采用的缩写

我们定义dispatch 函数 模拟 virtual dispatch过程:
该函数用于找到类所调用的具体函数方法
若为抽象函数或者不存在同名函数则一直用父类调用该函数进行查找(也就是继承函数的情况),直至找到第一个满足的非抽象函数方法为

以下示例分别展示了派生类赋值给基类,以及派生类覆盖基类成员函数的情况

Class Hierarchy Analysis(CHA)类层级分析
根据 declared type of receiver variable,也就是 receiver variable 的声明类型来找到所有可能的调用方法
receiver variable 可以简单理解为被赋值的那个,比如说下图的 a

cs 代表 call site
算法:
求解的T为函数签名集合

static call:

special call:

三种情况:构造函数,私有方法,父类方法
父类方法:

构造方法,私有方法基本和static call一样

dispatch的参数所给的类名是唯一的,返回值当然也是唯一的。
virtual call:

对c本身,和 c所有的子类以及子类的子类等(继承树上的所有子类)**c ‘**,都调用 Dispatch (c’,M),将返回值加入T当中。
注意dispatch的定义,只有调用dispatch才会可能去找父类,而virtual call的for循环用于找子类
如果继承类自己实现了函数且没有子类,那么就会对自己调用dispatch,从而找到自己的函数
如这种:

我这里就以基类调用派生类函数方法理解了(基类声明虚函数,我java不太行,用cpp理解了),需要遍历其所有继承子类才可以知道最终调用的是哪个函数方法
题外话,通过cpp补点java基础:
一、Java中的虚函数
普通函数就是虚函数(同等于C语言中virtual关键词修饰的方法)
虚函数的存在是为了多态
C++中普通成员函数加上virtual关键字就成为虚函数
Java中其实没有虚函数的概念,它的普通函数就相当于C++的虚函数,动态绑定是Java的默认行为。如果Java中不希望某个函数具有虚函数特性,可以加上final关键字变成非虚函数
据统计Java的:静态方法、私有方法、final方法、实例构造器、父类方法都是非虚方法,除此之外都是虚方法
二、参考
C++虚函数 == Java普通函数
C++纯虚函数 == Java抽象函数
C++抽象类 == Java抽象类
C++虚基类 == Java接口
https://blog.csdn.net/trojanpizza/article/details/6556604
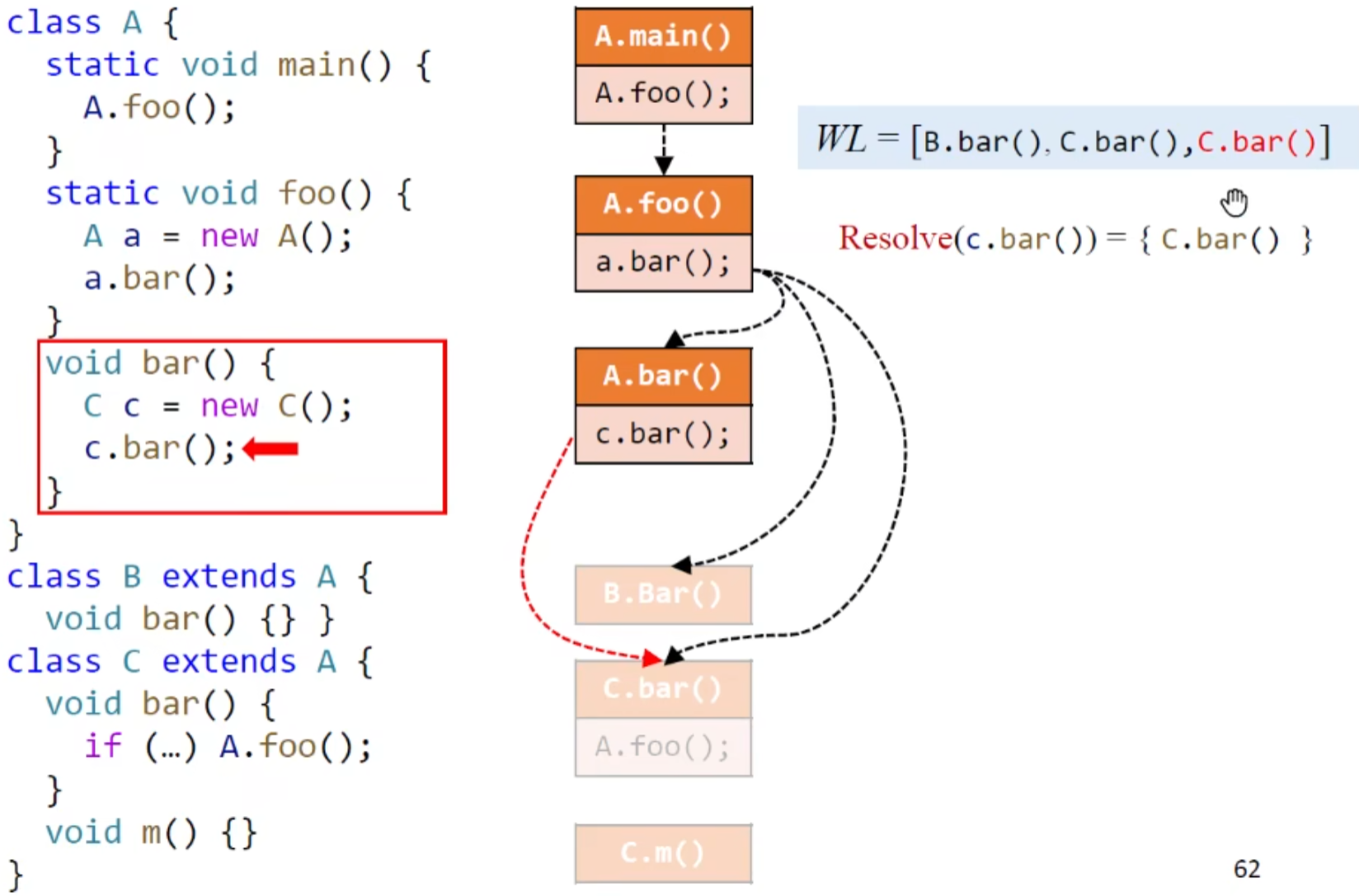
示例:
这里有一个比较容易漏的地方:
B类自身没有foo函数,故既需要向上(也就是找继承父类的函数),也需要向下(找子类实现的函数)
其实也就是对应了前面算法的:1.对B本身进行dispatch,返回A.foo 2. 对B的所有子类进行dispatch,返回C,D的foo
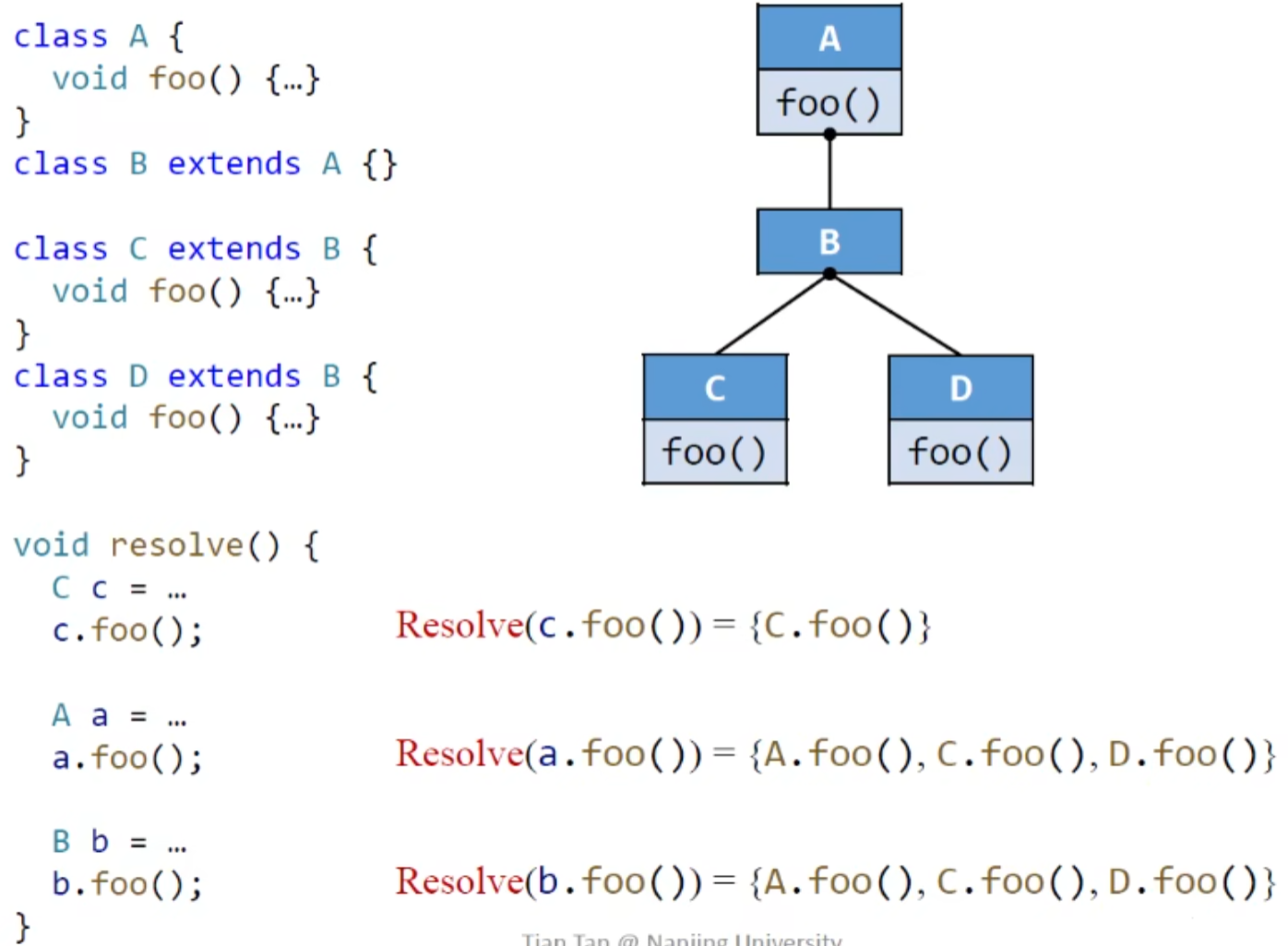
此处具体为new B也是一样的,这里弹幕答错的人有点多,感觉可能是没好好看CHA定义?毕竟定义就说了只关注类的声明类型。不过这里也暴露了CHA的不足,毕竟程序运行的话是不会调用C,D的foo方法的
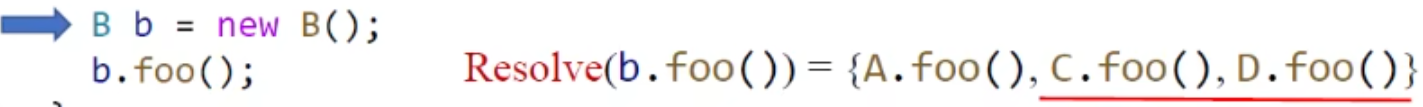
CHA特点:
1.速度快
只考虑调用点 receiver variable 的声明类型
忽略数据流,控制流信息
2.不精确
很容易引入冗余的调用方法,如上图示例
可以用别的方法避免这个缺陷
现代IDE找call site就有用到CHA,毕竟速度快,反应的结果也是给人看的
老师给了IDEA的例子:
与上图例子相同,使用了CHA,不够精确
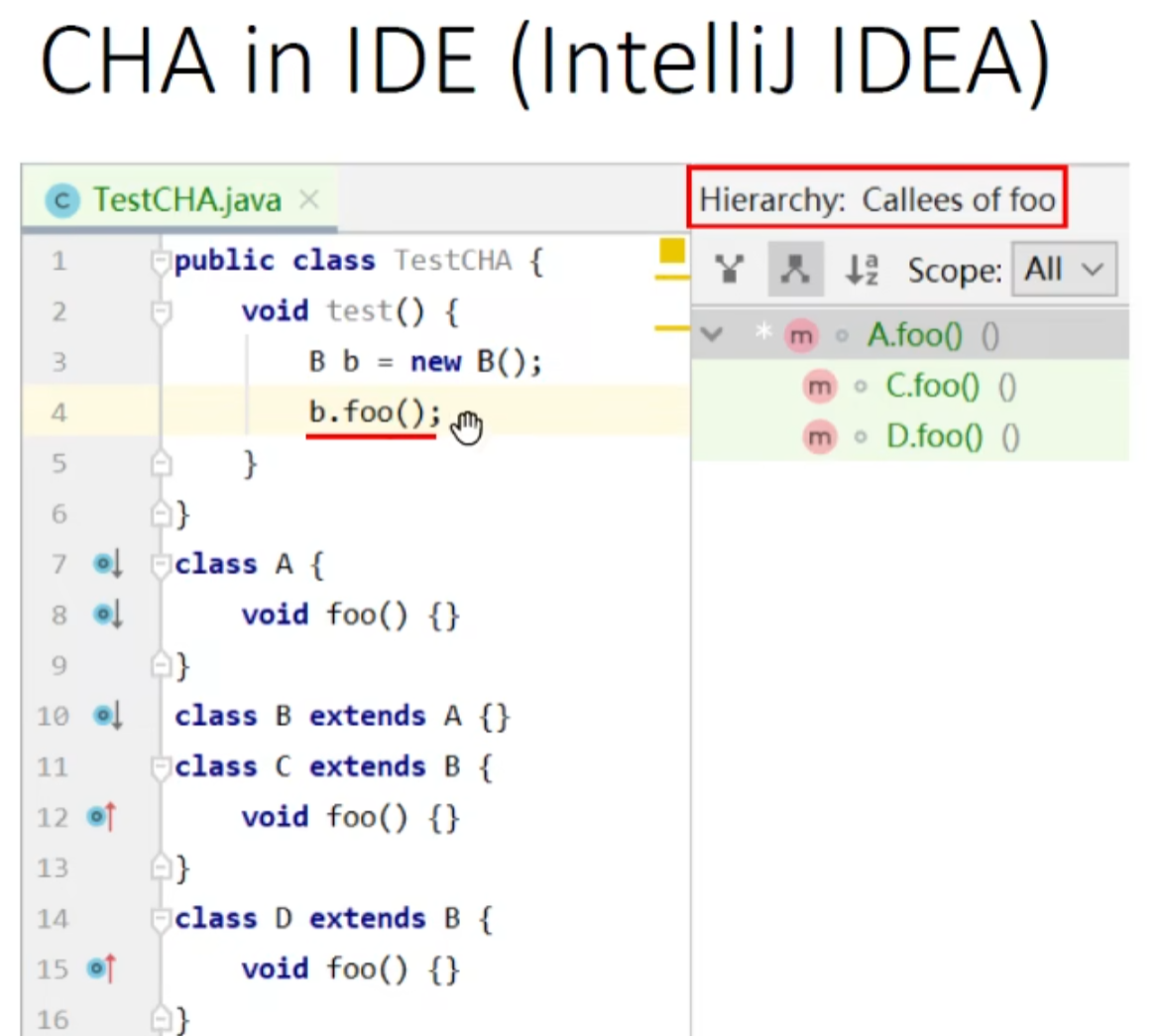
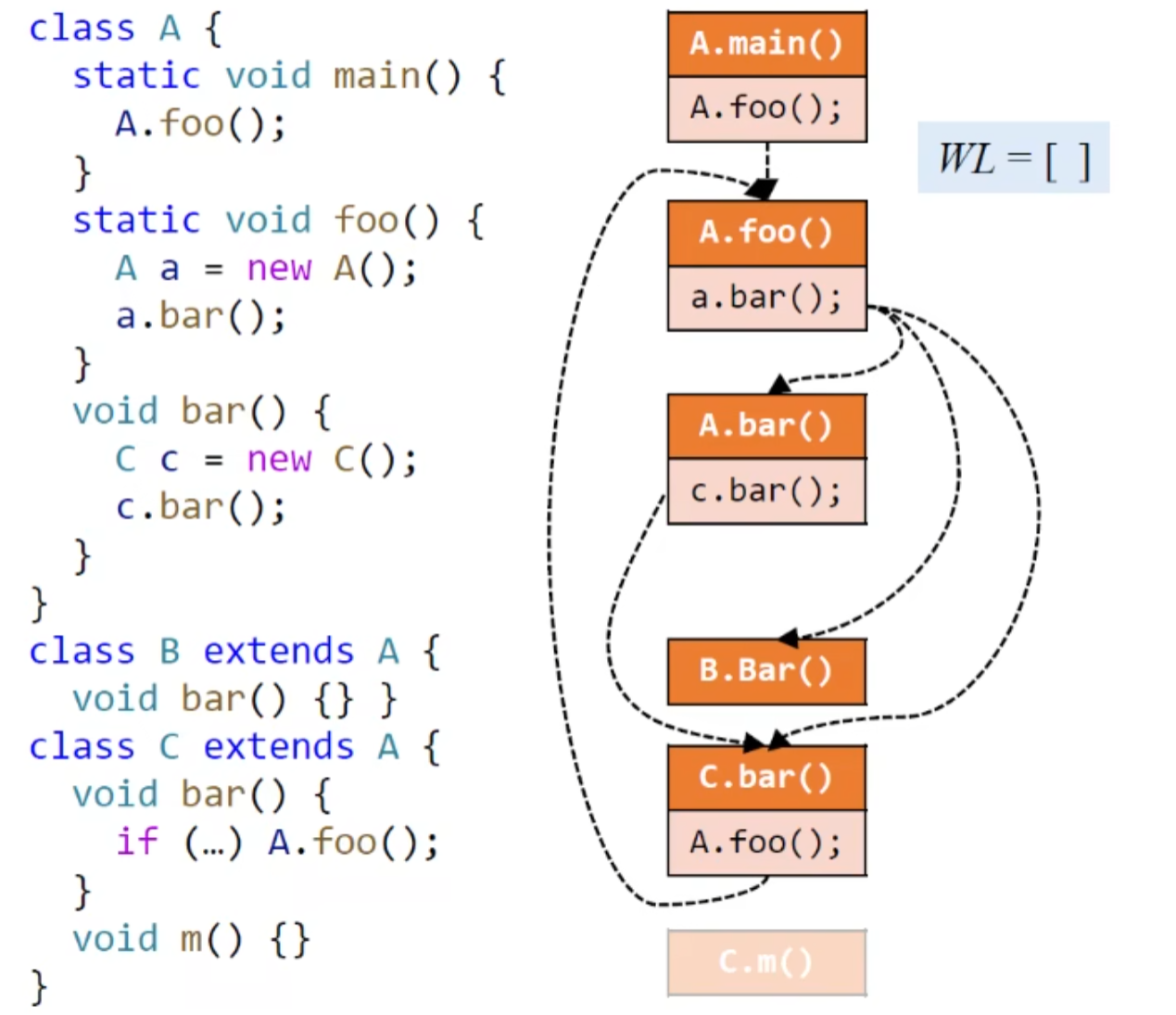
使用CHA构造call graph
对每个调用点应用CHA,一直重复直至没有新的方法被找到(有可能存在有些方法是不可达的就跟数据结构学的构建图差不多)
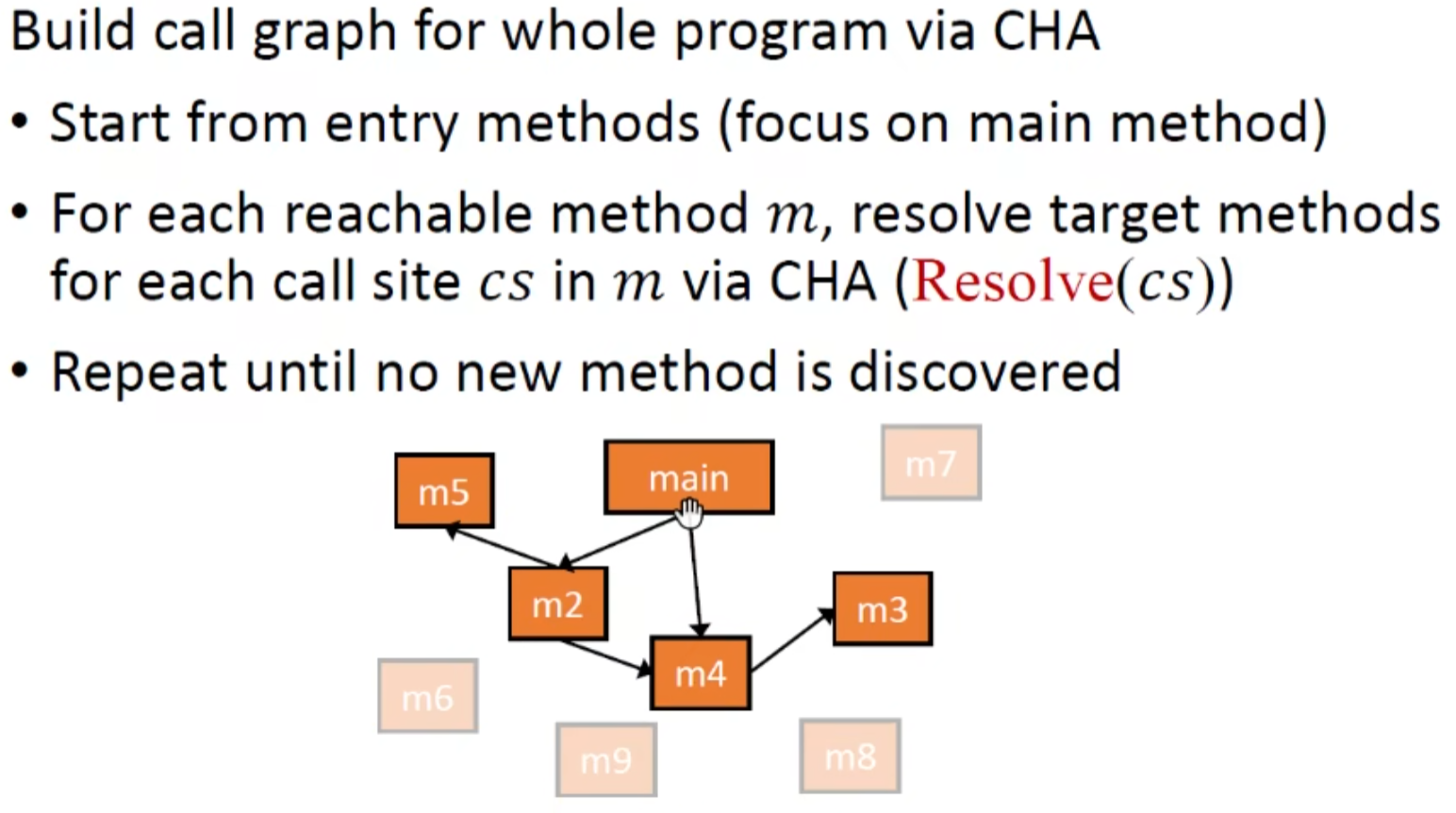
算法: 相当简单粗暴的worklist,算法思想有点类似于BFS,以所有main函数内方法为worklist,不断从worklist中取方法,然后又加入新的方法这样
RM集合用于优化,可以在遇到以及处理过的函数方法时直接快速进入下一次循环

示例:
跟个算法走一遍就行了,很好理解
Interprocedural Control-Flow Graph (ICFG)
ICFG = CFGs +call edges + return edges

retrun site可以理解为紧跟着call site的下一句

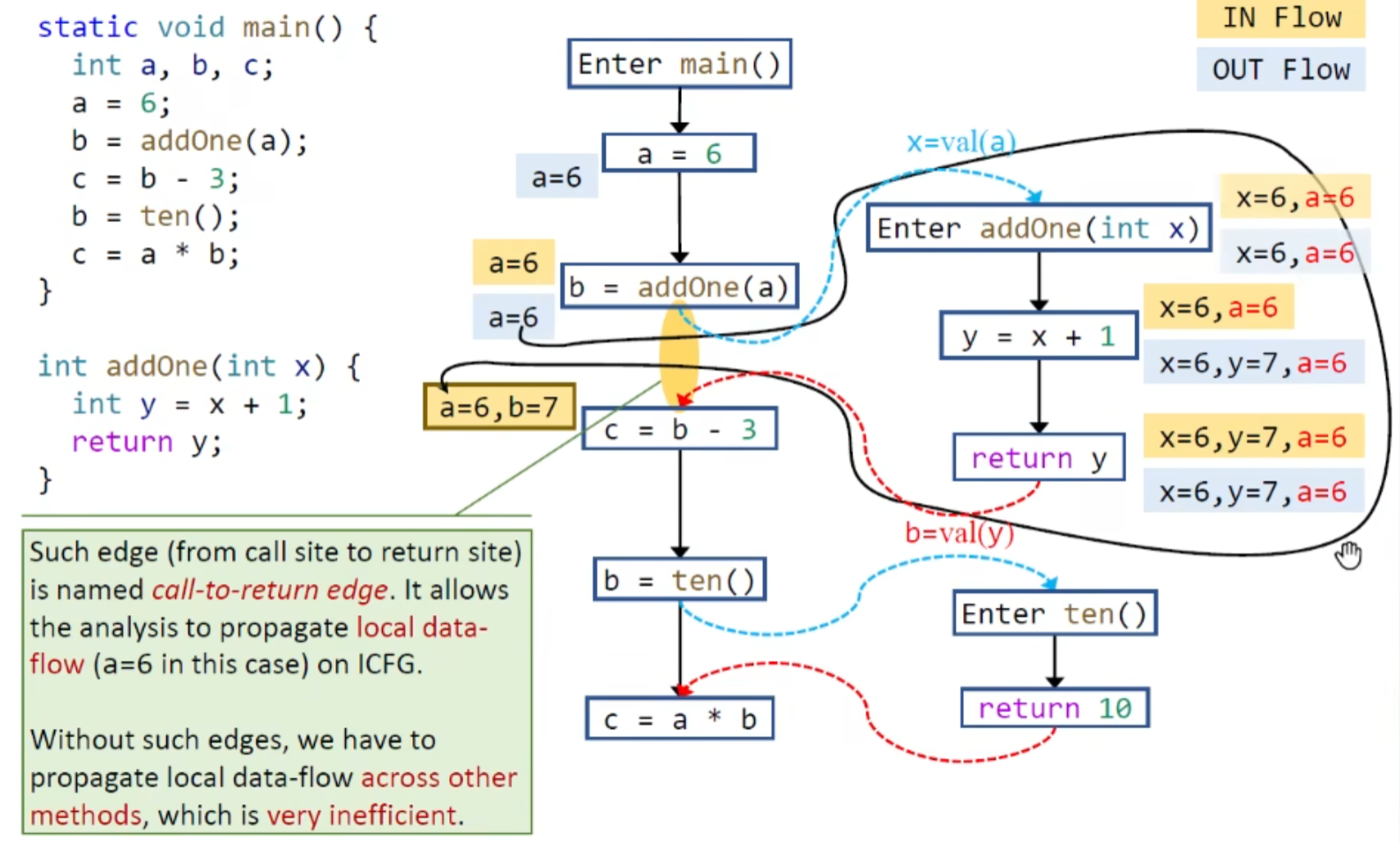
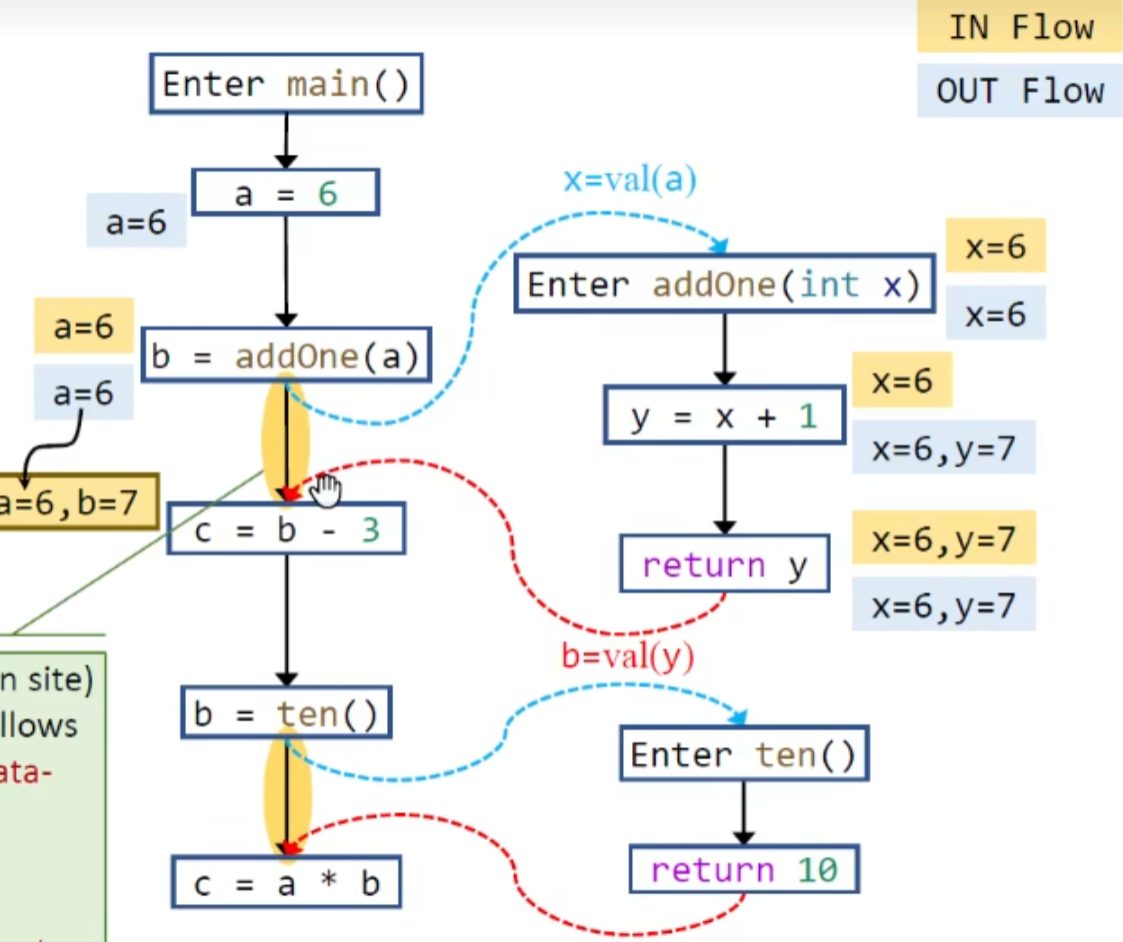
ICFG示例:
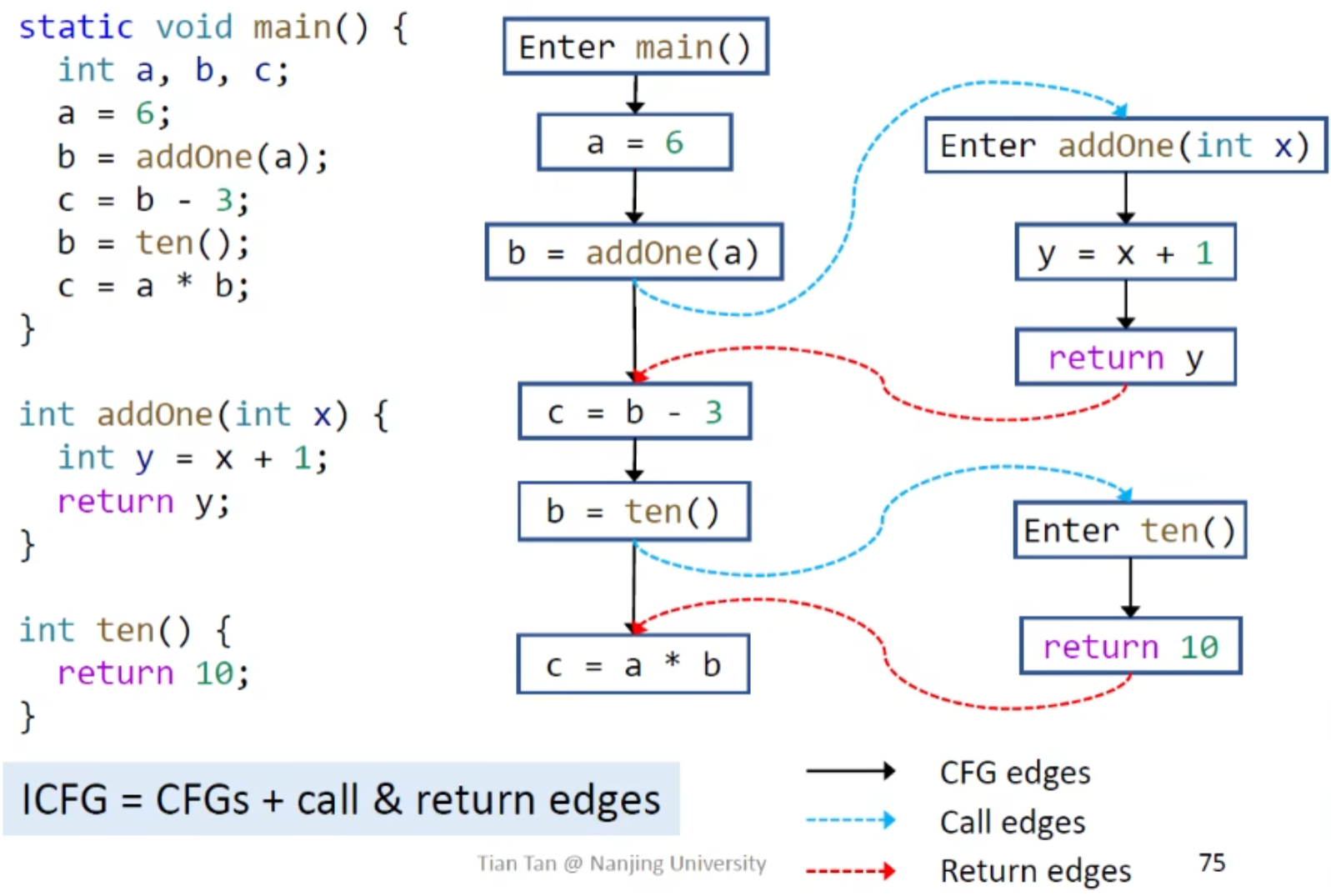
这里有个问题就是有了调用边返回边,为什么还需要CFG的那条边
解释:
这里只考虑值传递(不考虑引用传递),这条边可以传播本地的数据流
如果没有这条边的话就会这样:
目标方法中会有额外的变量,这是没必要也不应该的
故需要这样:
过程间数据流分析
分析建立在整个程序基础上的ICFG,但没有标准的做法
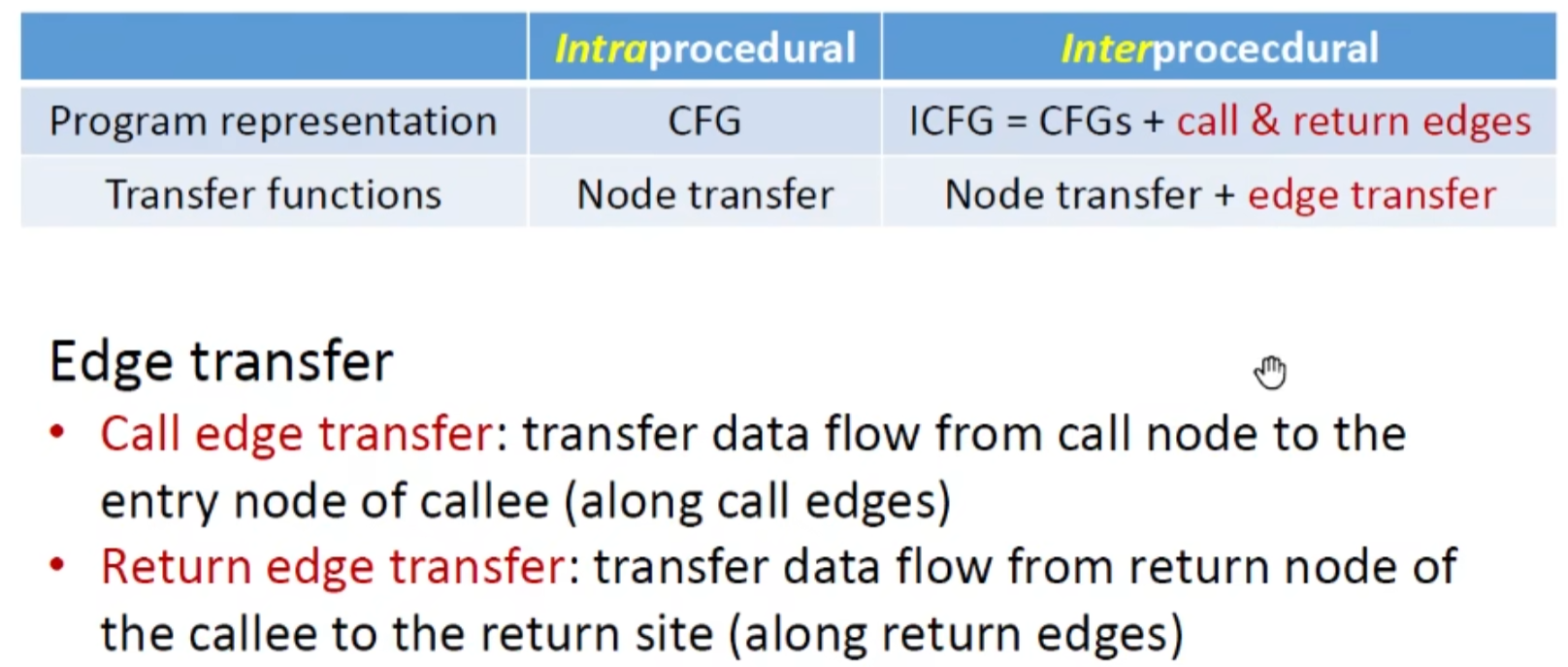
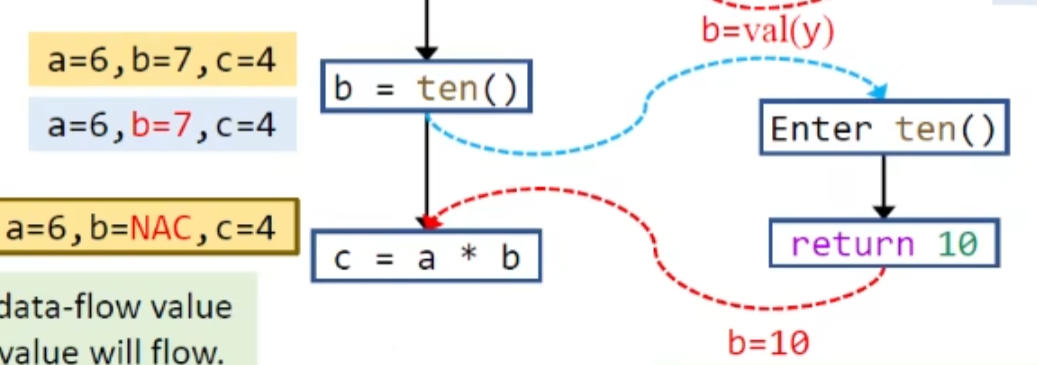
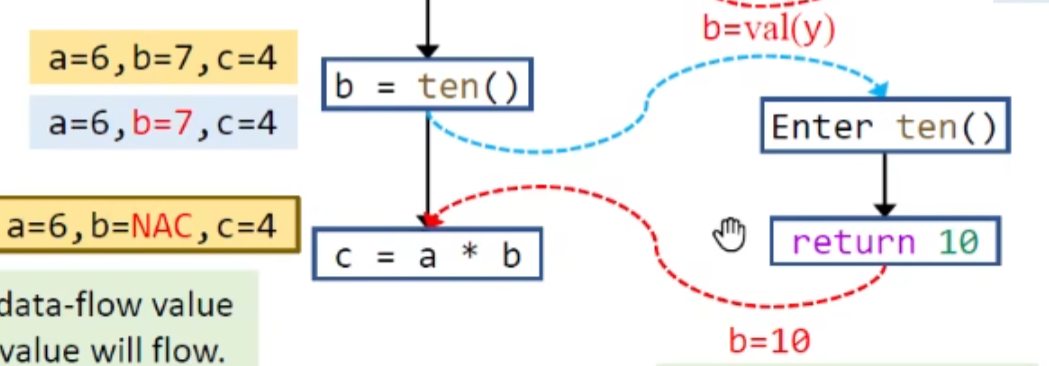
在node中数据流分析时,要去掉call site处的左值(赋值语句的左边,因为此时该值还未确定),其余与过程内分析相同
如果保留的话,数据流在meet join时就有可能出错:
这个b=10应该能覆盖原值才对,kill掉就能避免这种精度上的损失:
call edge则传参
retuen edge则传返回值
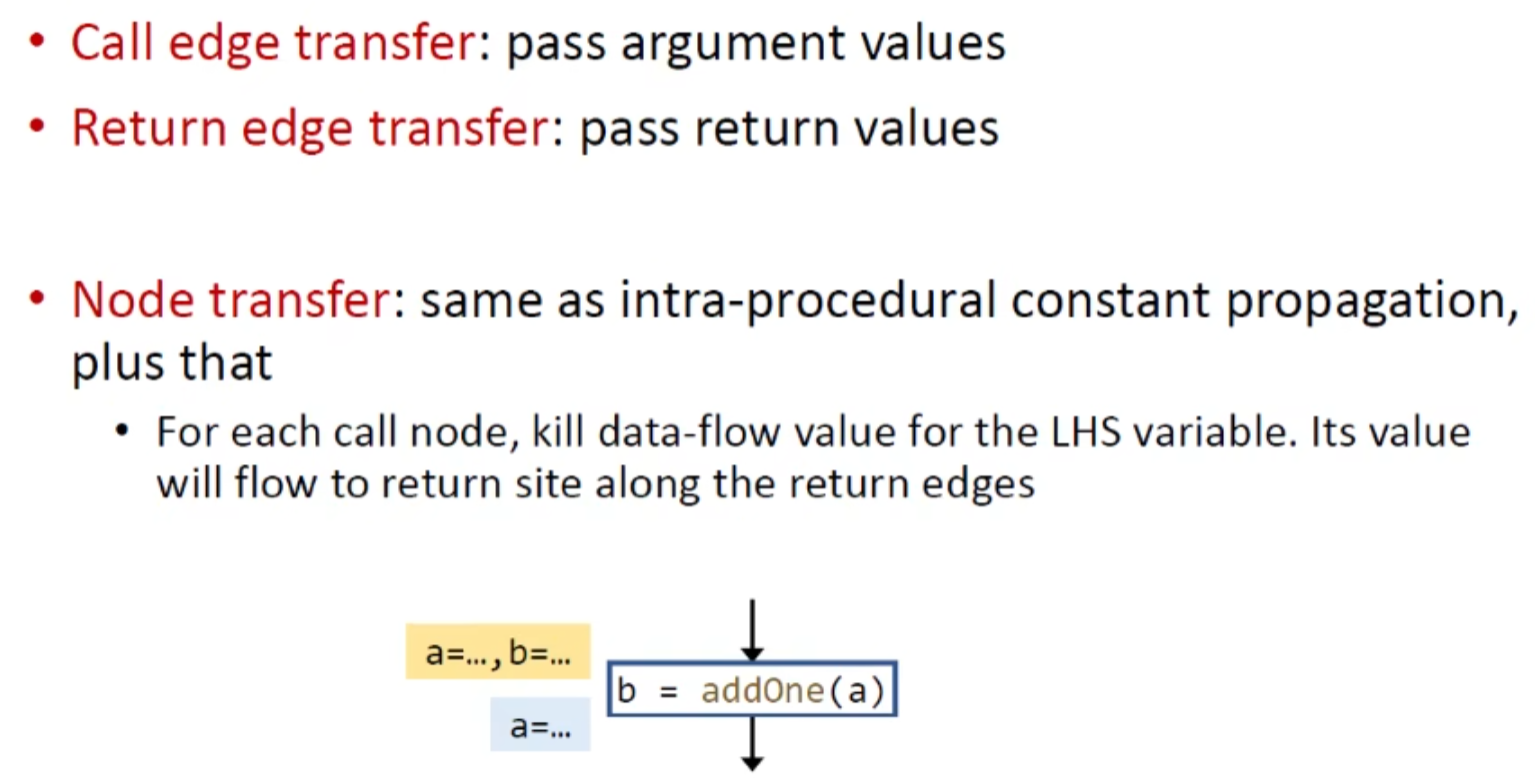
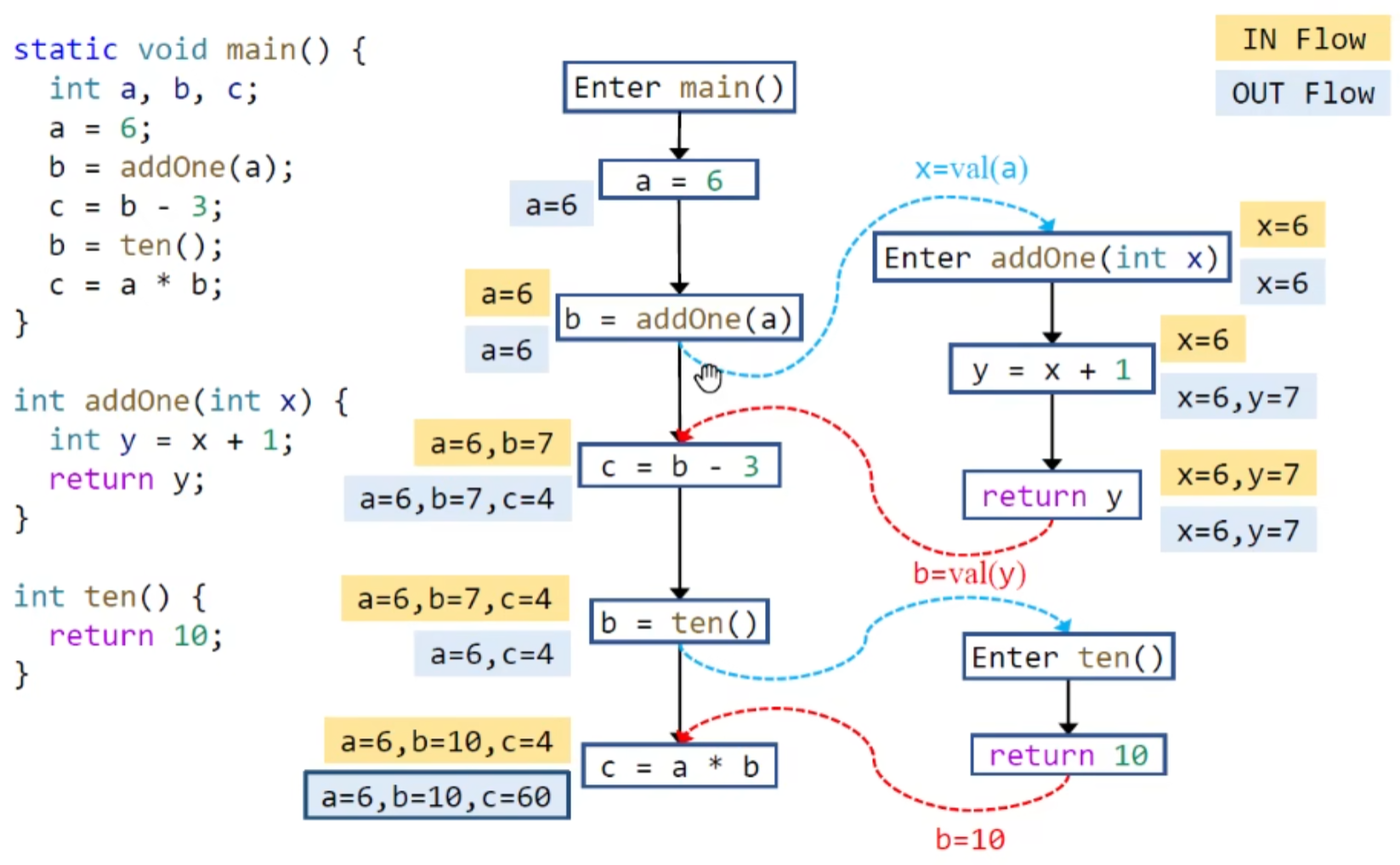
以常量传播为例:
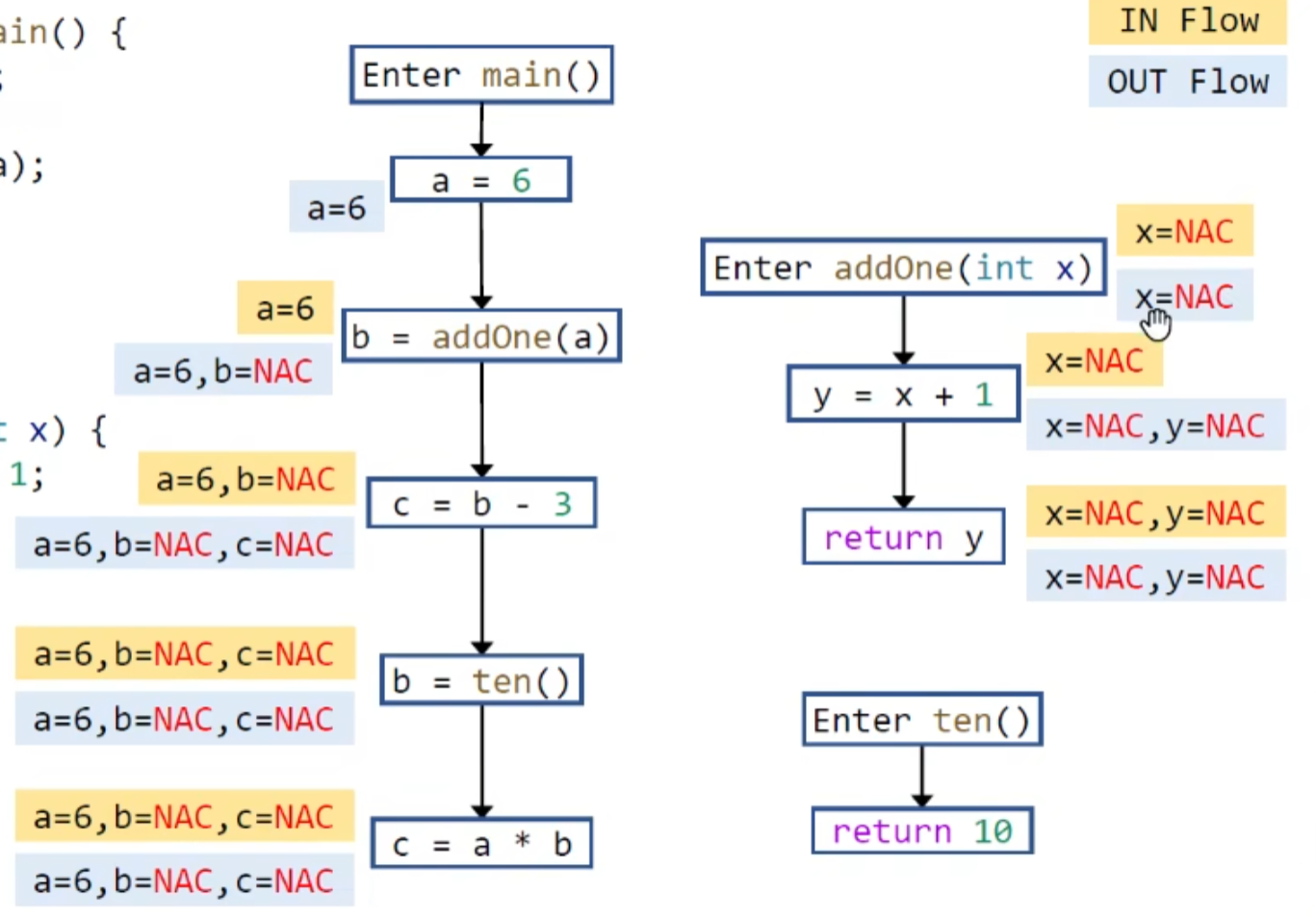
过程内分析会做最保守的假设,十分不精确:
Poniter Analysis
只能说指针分析这部分是这门课学起来最难受且有些枯燥的
为什么需要指针分析?以CHA为例,CHA只考虑了调用者的类型,在以下常量传播中会给出非常不精确的答案,若用指针分析的话就可以解决这类冗余调用边的的问题:

introduction
定义
计算指针具体指向的内存

例子:

别名 Alias
指针p,q指向同一个对象就称为别名
别名分析和指针分析相关 但是不讲

应用
与安全相关的,空指针分析,以及程序流分析等

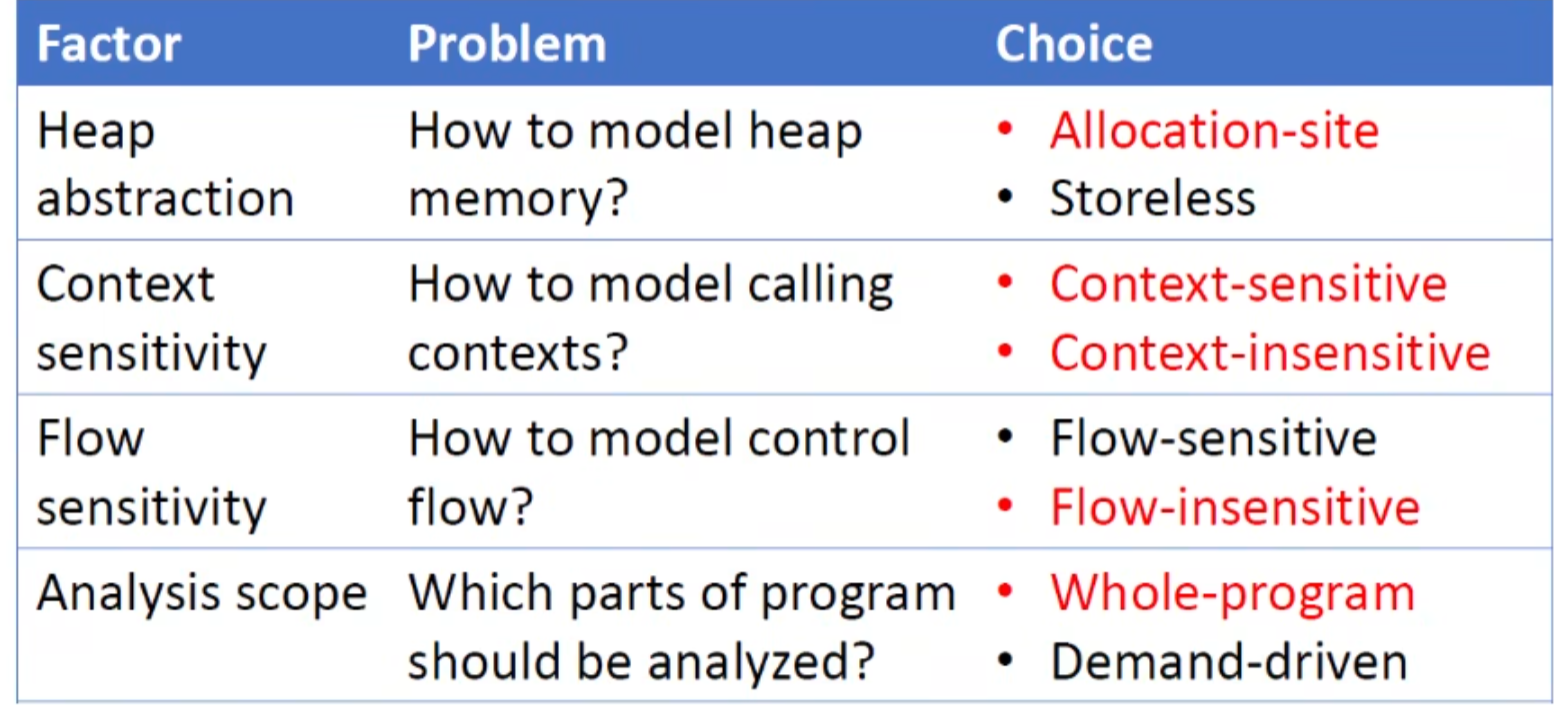
关键要素
对于不同的场景有不同的选择
- 堆抽象
- 上下文敏感/不敏感
- 流敏感/不敏感
- 全程序分析
标红的是我们将要学习的
heap abstraction
对于循环/递归产生的大量堆指针对象,抽象相似对象 合并为一个对象便于静态分析(限制处理对象的个数,保证静态分析可以终止)
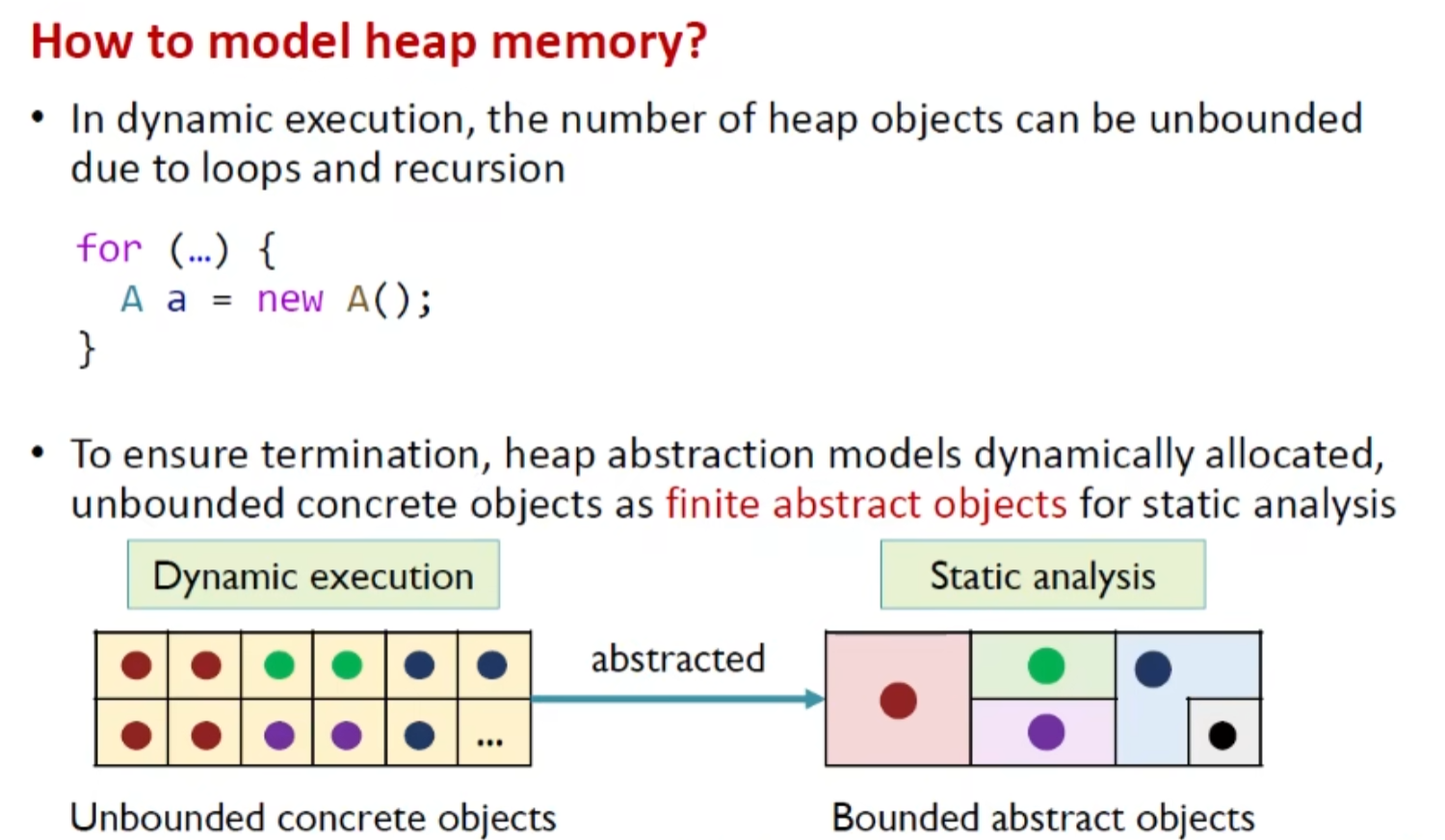
两大流派:store based/storeless model,以及他们的混合流派
我们学习store based下的allocation sites ,因为最常见,最实用/有效(对java)
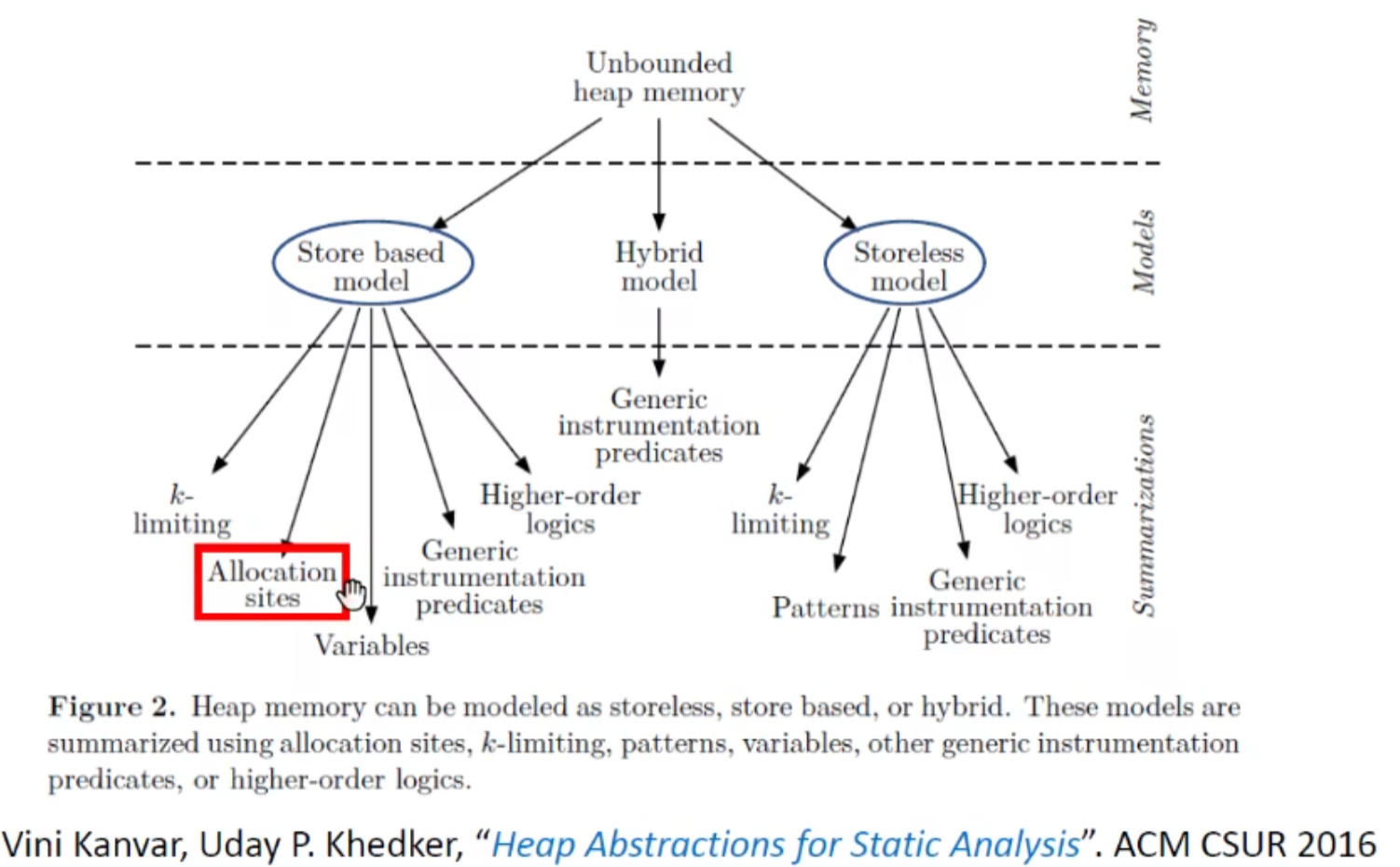
allocation sites abstraction 创建点抽象
意外的挺直观,(简单来说有几个new语句就会处理几个对象)

context sensitivity
上下文敏感:模拟动态执行,对同一方法的不同上下文调用,分开分析 (更精确,对java提升很明显)
上下文不敏感:汇聚在一起分析,只分析一次
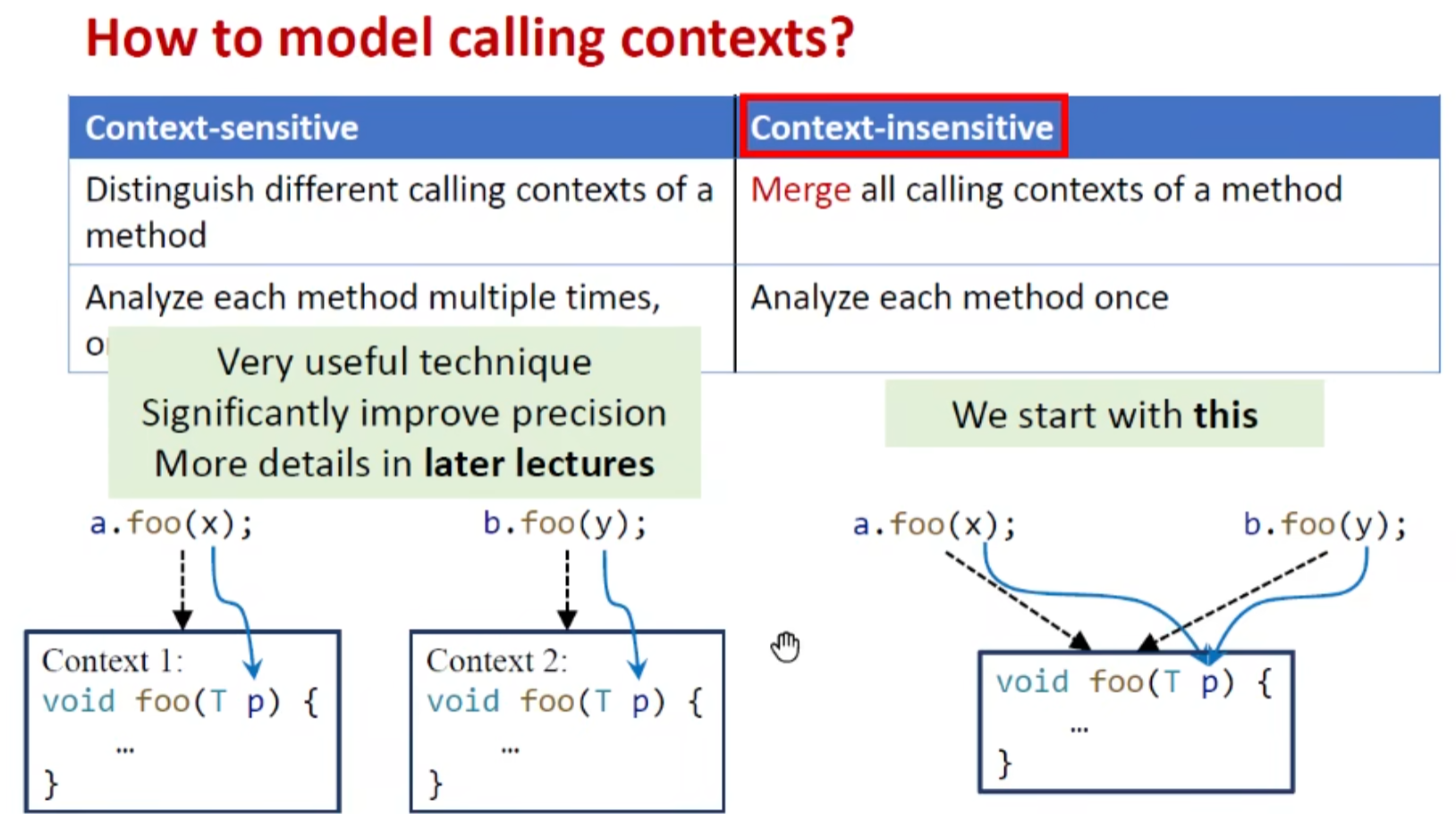
flow sensitivity
主要考虑怎样对控制执行流进行建模
我们前面学到的那些data flow 数据流分析都是流敏感的
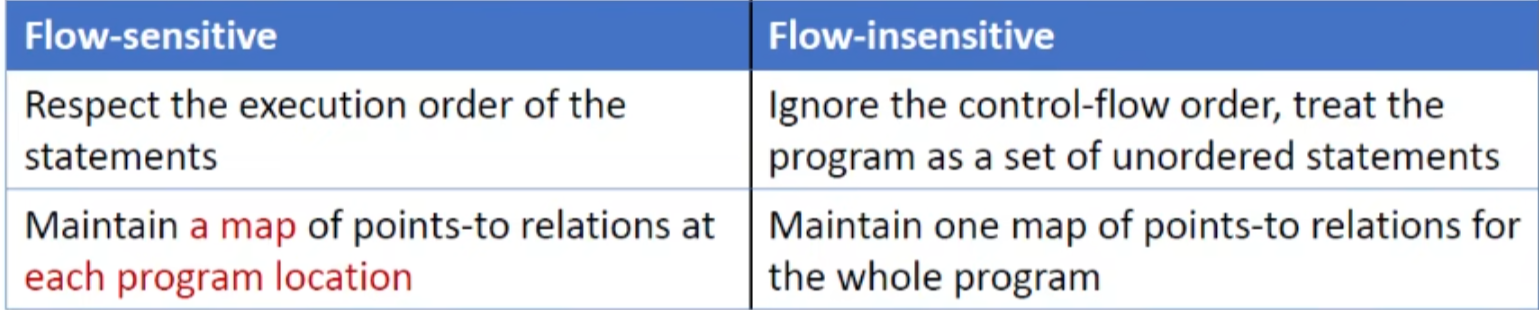
通过在程序每个位置维护一个指向图来实现流敏感,非流敏感则在整个程序中只维护一个指向关系图(不考虑控制流执行顺序)
流敏感/非敏感比较:
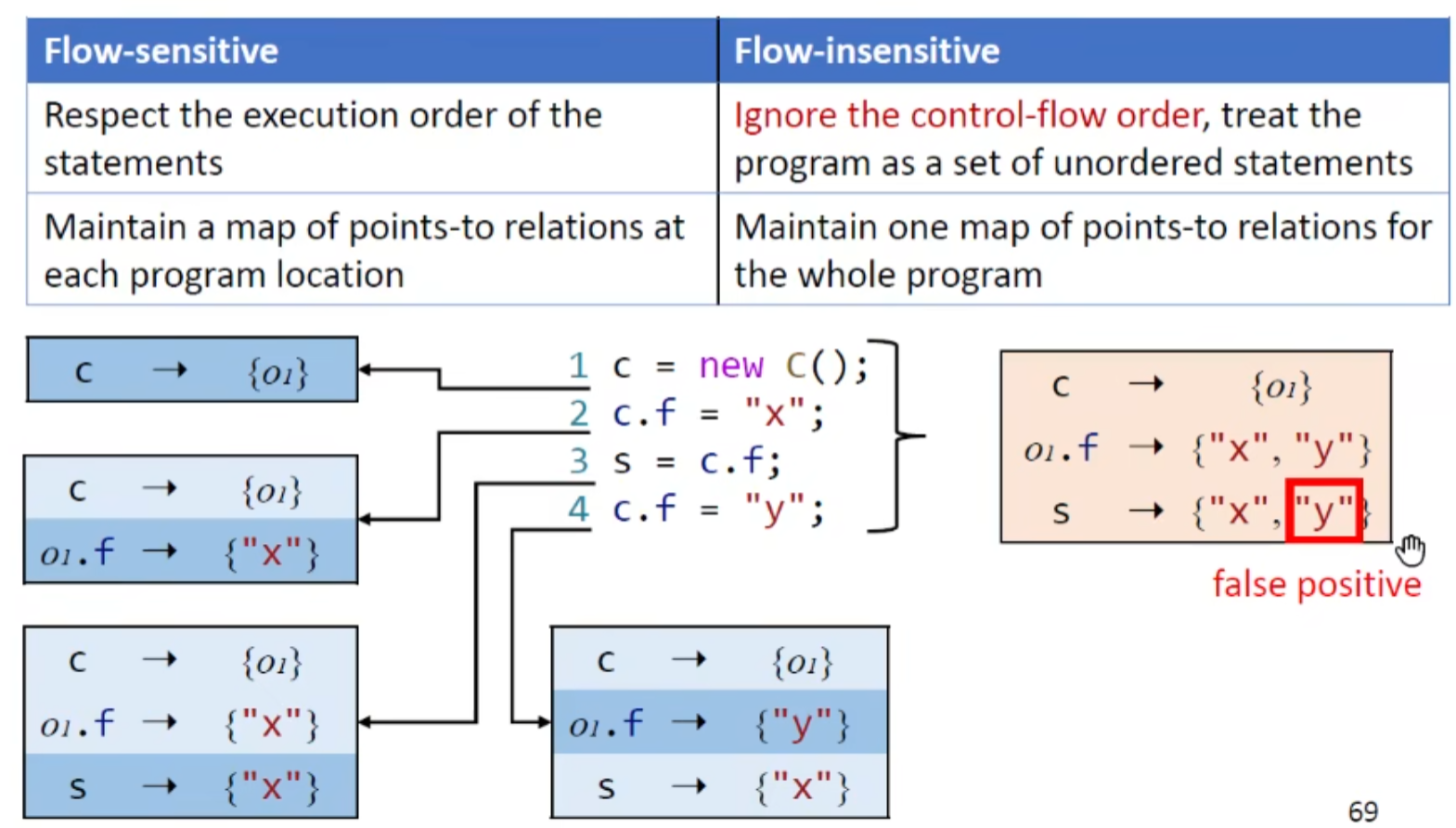
对C类的语言的流敏感分析非常有效(精度提高),但目前没有研究表明对java的流敏感分析能显著提高精度
Analysis Scope
简单来说就是选择需要分析的对象,需求驱动的分析就只分析部分指针(计算量更小,但不一定会小很多),否则就是全程序都分析(主流,适应几乎所有情况)

关注对象
只考虑影响指针/指针相关的

以java为例:
对于数组的分析,我们忽略下标,将数组当成单个的指针对象来看待

那么大概就是关注5类语句:
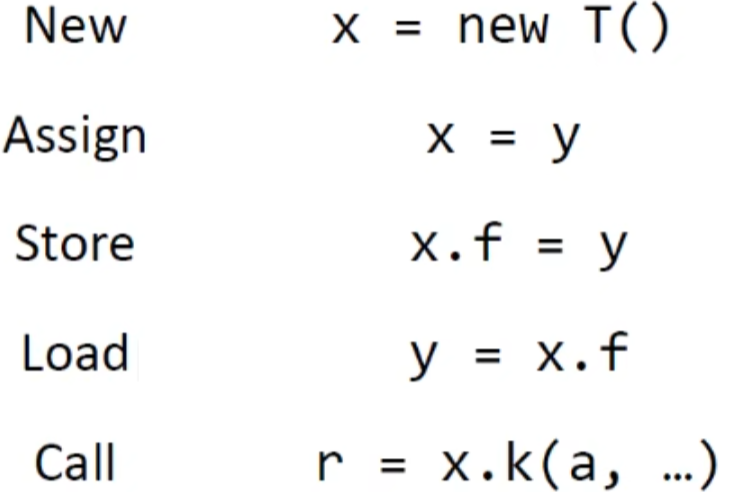
call就是之前call graph例子中的三种:static call,special call,virtual call(重点)
对于多重指针,会使用3AC简化:
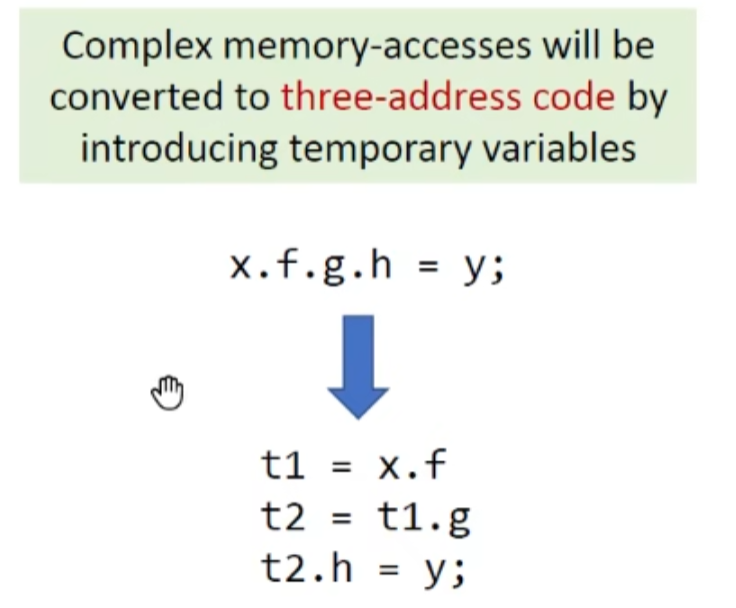
Foundation
域/符号(domains/notations)
指针域 可以理解为 变量域 + (对象域 × 实例对象域)
pt可以理解为映射关系(函数)

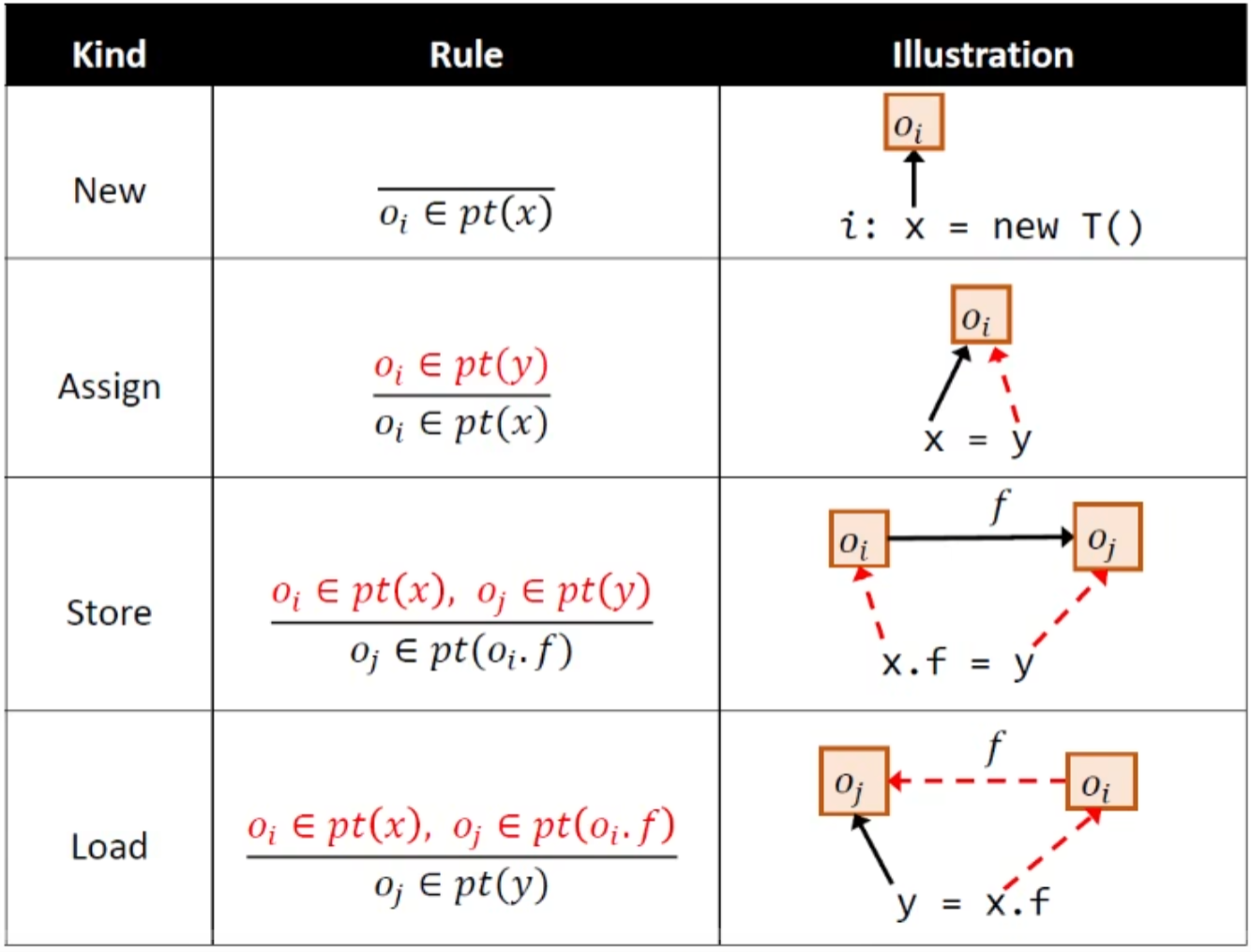
Rules
以下的rules不考虑不考虑call
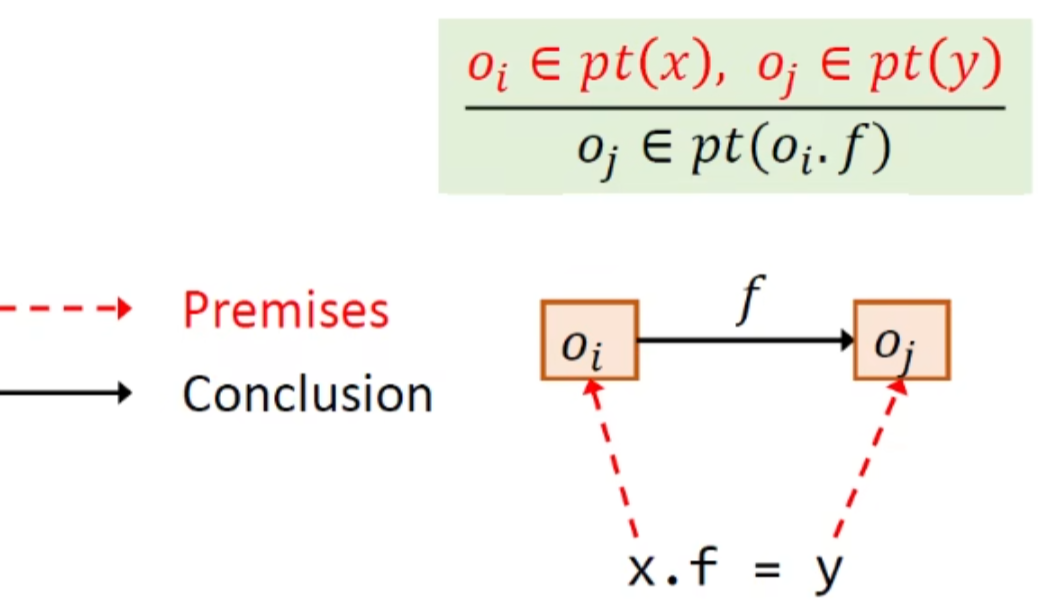
集合关系都挺好理解的,以store/load为例子(理解这两个其他就都理解了)理解一下关系图和符号就行
premise为前提,conclusion为推导结论
store:
load:
以store为前提的推导,结合store就很好理解
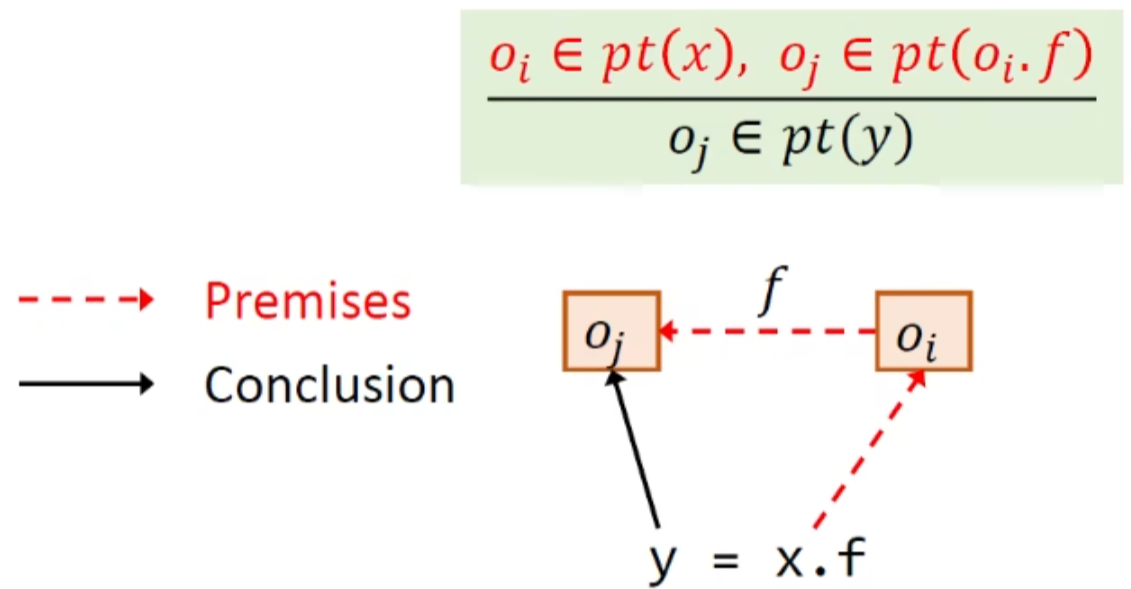
总览图:
分析有点类似传播信息,本质上可以看作是对包含关系的约束求解

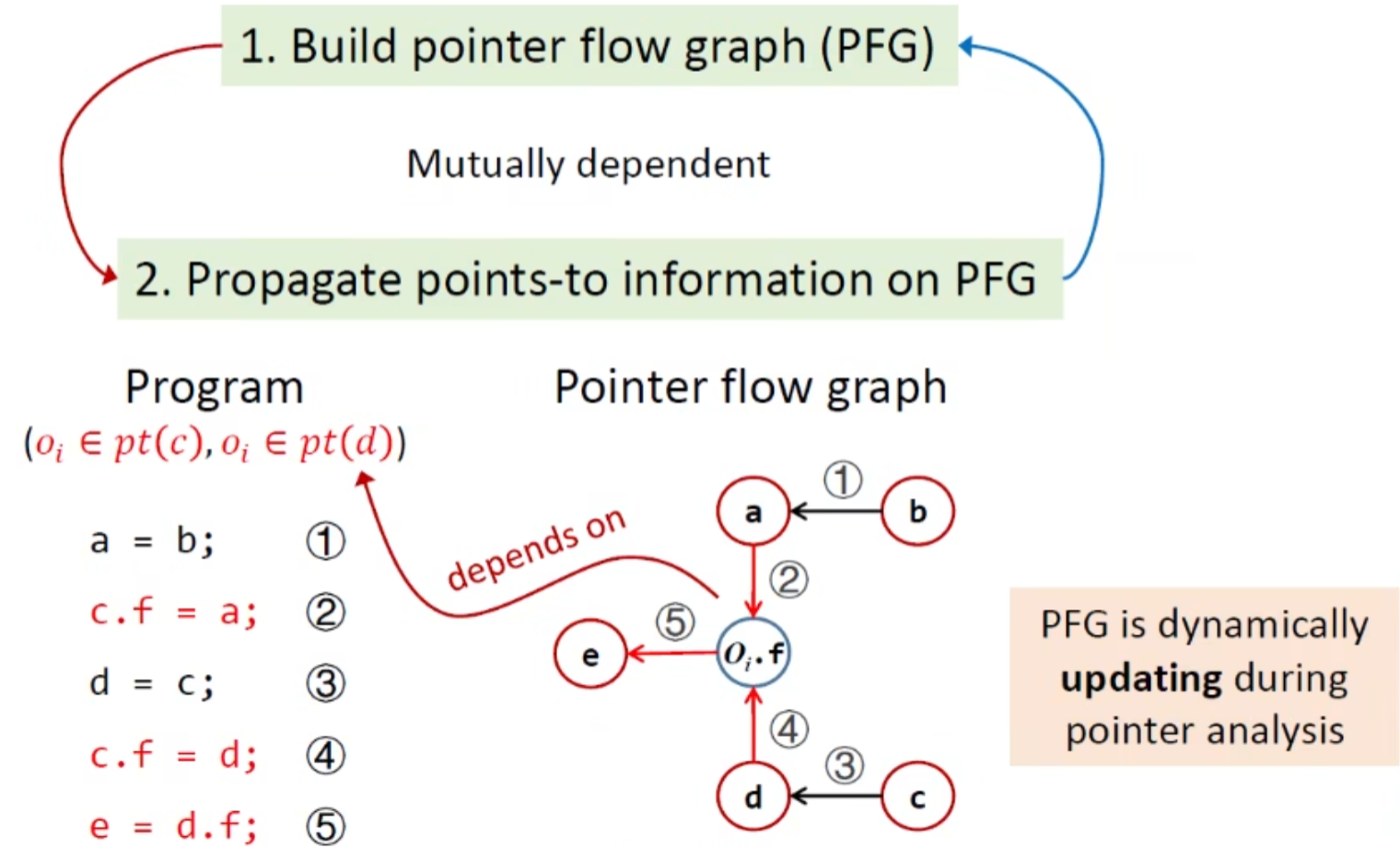
Pinter Flow Graph(PFG)
节点nodes即为程序中的指针,边edges代表指针对象之间的流动关系

边符号表达,可以理解为信息传播:
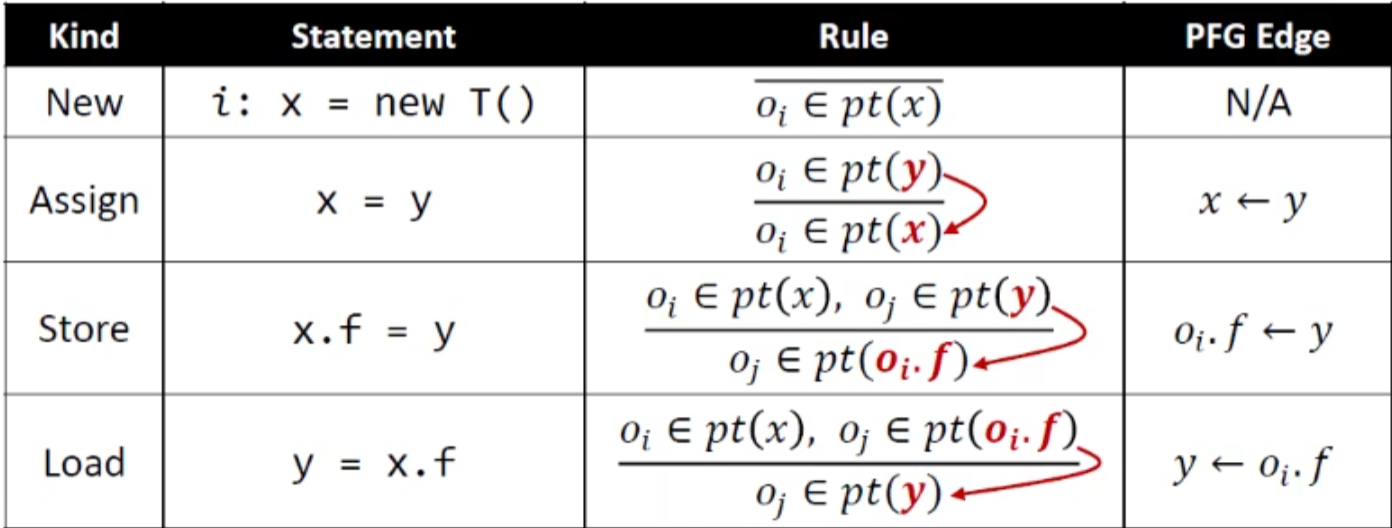
示例:
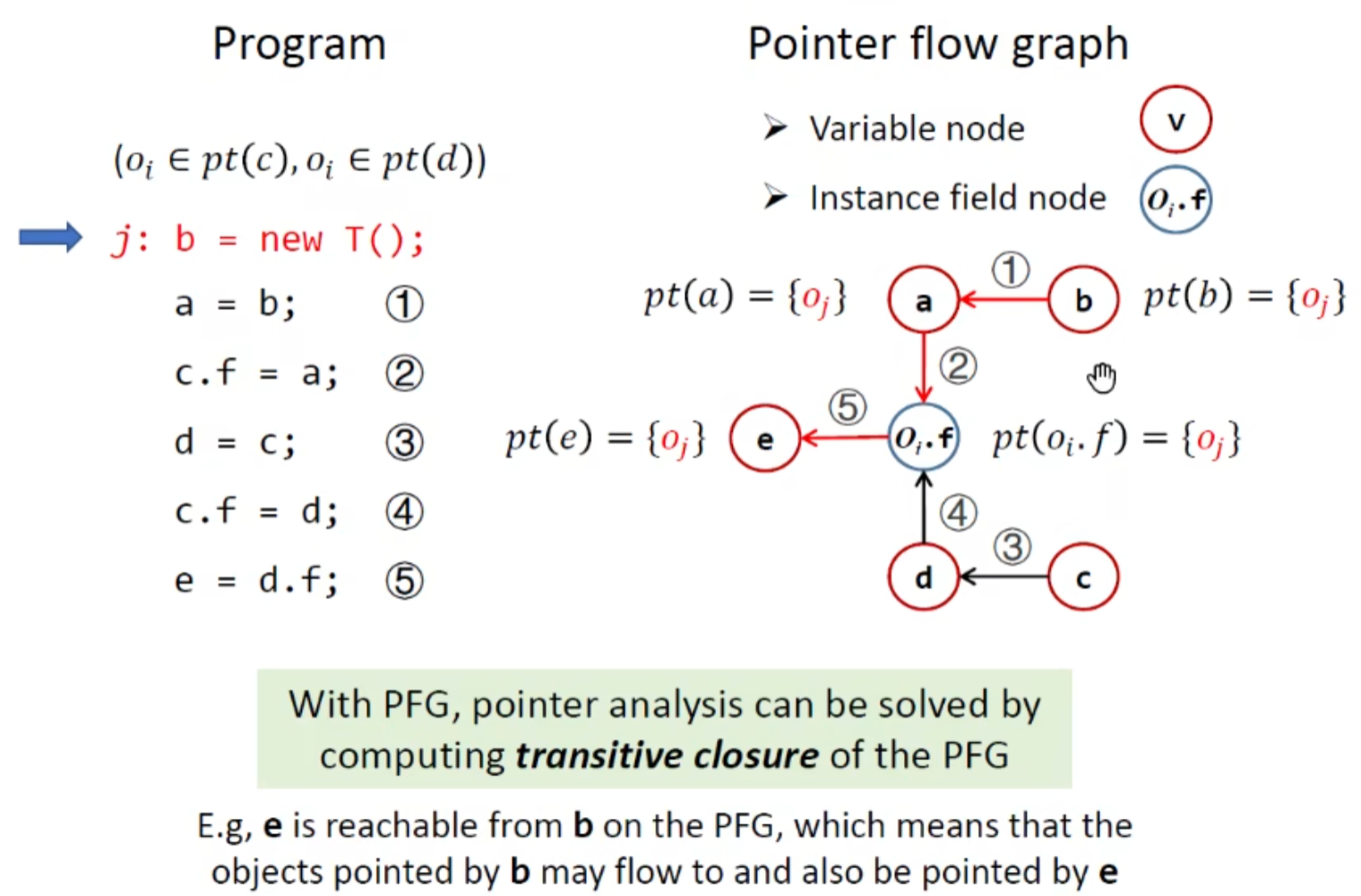
这样算法就可以抽象为在图上指针信息的传播,但并不是单单分析PFG的的问题那么简单,因为PFG的构建也依赖于指向关系信息
Algorithms
算法总览:(不考虑call语句,只考虑4中语句)

worklist和前面的worklist类似,存放我们需要处理的指针信息
每个entry以pair的形式 <指针,指向的对象> 存储

new && assign
这两种情况比较好理解,先处理所有的new作为初始化,再将assign边加入
这里assign addedge的处理要保证集合能包含右值(也就是**确保满足pt(y)包含于pt(x)****),所以AddEdge最后需要有一个add worklist操作

worklist处理:
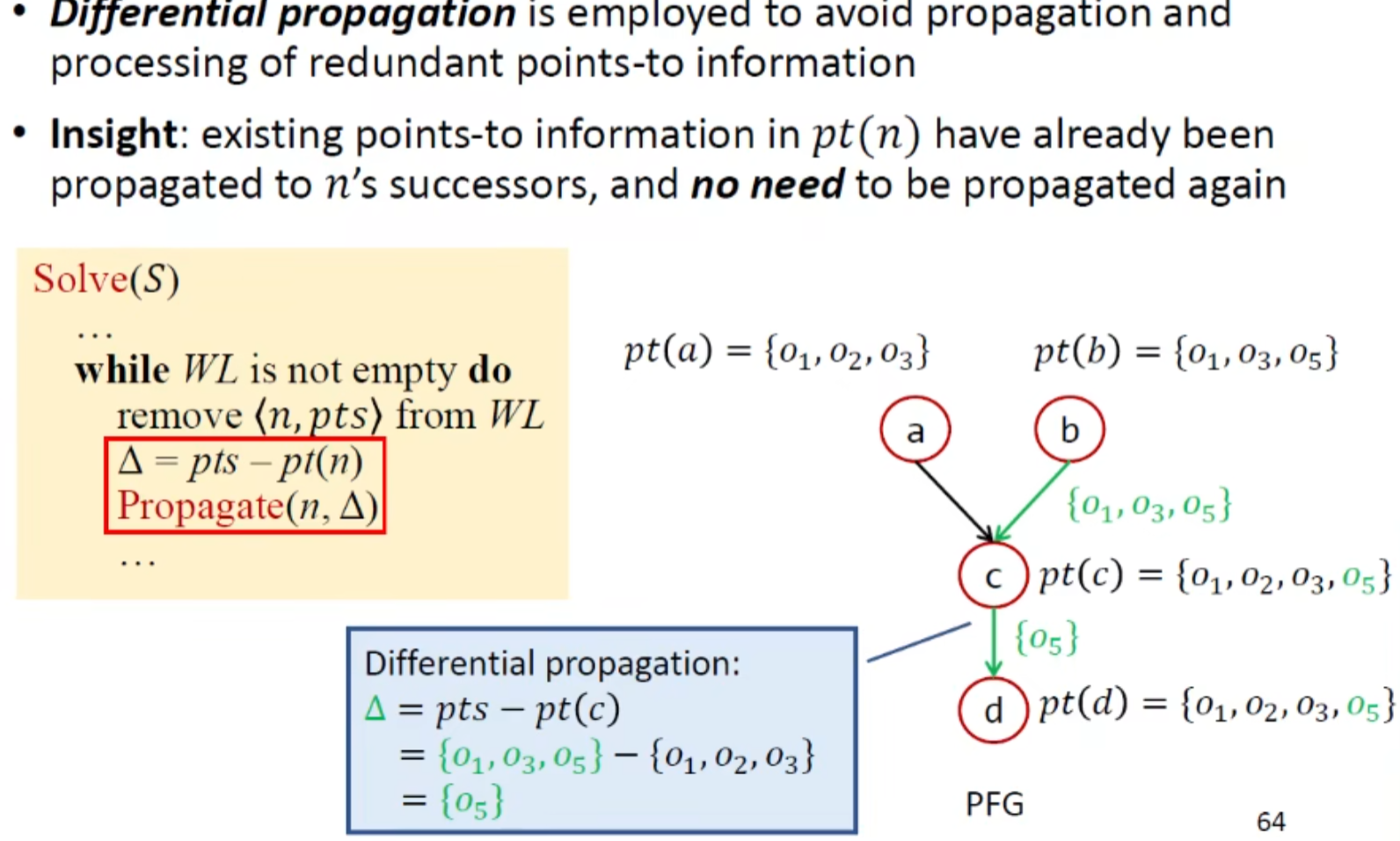
从队列中取出一个entry,计算出 需要被增加的那部分集合(也就是要减去原有集合的部分,算出来是真正需要传播的部分,本质上就是去重),然后调用Propagate(传播)处
为什么要去重这步操作?
这是从实际工程的角度考虑的,差异计算主要就是避免冗余操作(多次处理重复指针)
除了上面这里,在后面的foreach循环中也有优化效果
Propagate:
修改就是一个简单的并集(如果不是空集的话)
然后需要对被修改的指针的所有后继都进行修改(通过PFG可以查找后继,对后继进行修改也就是沿着PFG传播)

store && load
这里感觉比较模糊,我一开始比较不理解的地方就是 store/load 为什么是对 Δ进行处理就行,pt(n) 到底是在哪里处理过了
事实上算法是个流不敏感算法,本质上就是先处理完new && assign语句进行初始化,然后再对worklist中出现的变量一一处理:worklist中的变量存在store/load的话就进入foreach循环,那么对于一个变量的load/store语句,就是第一次遇见该变量时处理的,此时的Δ就是pts,pt(n)为空集 ,这样就搞清楚了。

示例:
谭老师详细讲述了整个过程,这里跟着视频走一遍算法或者看ppt就很好理解了(第九讲)

处理call语句
分析call语句需要建立在call graph基础之上(不然的话不知道往哪传播),而用我们之前学习的CHA来建立call graph会有冗余的信息,我们使用指针分析来计算call graph,这样比起只关注声明类型的CHA更精确
这与之前的PFG类似,call graph也是分析中建立的,我们称为 on-the-fly call graph construction

方法调用主要涉及:
1.找到目标方法(Dispatch)
2.传目标方法
3.传参
4.传返回值
Rule基本也就是做这四件事

Dispatch定义与前面函数间分析基本相同,用于找到目标方法
在示例中就是找到T.foo()

传目标方法:把x传给this(也就是pt(x)中的oi传递给pt(this))
传参:类似传目标方法,对每个参数执行传目标方法的操作,将实际参数的域传给形参,可以往实参->形参加一条边

这里容易想到一个问题,为什么对this(传目标方法时)不像传参也加一条边来传递呢 x->this
因为x可能会有多个对象的方法调用,而receiver object应该只流向this对应的对象,考虑示例的情况:
A,B,C的this分别就是new A,new B,new C
如果加上了边的话,x的所有对象会沿着边传入this,这样ABC的this都会指向三个对象,然而对于A的this来说,不可能流向B,C当中,对BC也同理,这样就不会乱流,传递冗余的对象了
我们可以通过类型等方法判断this,故我们不连边,但我们根据参数就判断不出来具体的目标形参,只采取保守的做法,直接连边
传返回值:pt(ret)传给接受返回值的pt(r),加一条边

总览:

call graph和指针分析相辅相成,都是在过程中构造出来的,这样对指针分析是有好处的,逐渐形成的call graph将会是一个可达图
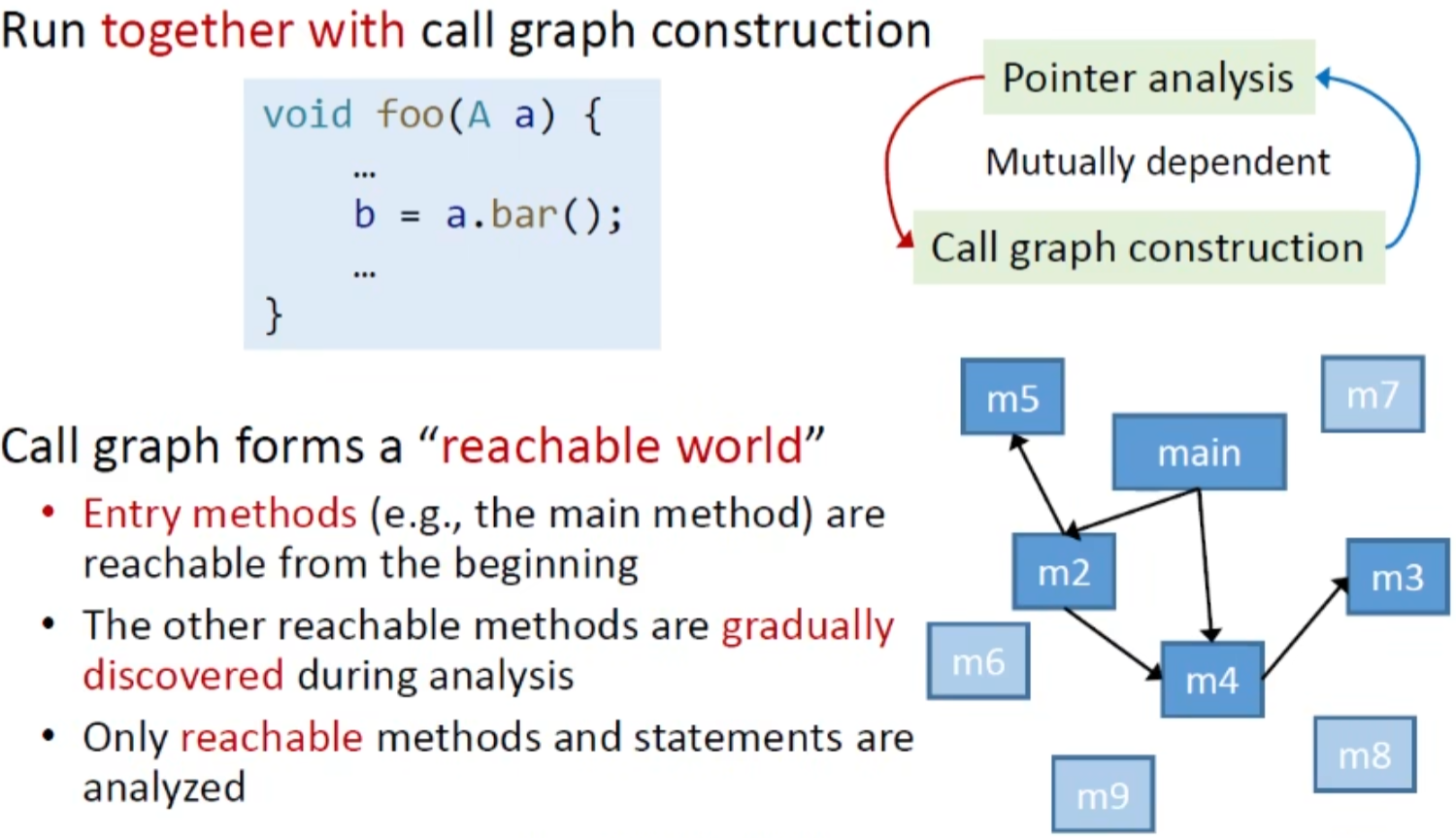
Algorithm (含call)
相比没有call的情况,多了call graph集合以及可达集合

AddReachable
该函数用于增加可达边,有两种情况:
- 入口方法可达,作为初始状态
- 新的call edge边被发现
一个新的方法m第一次被处理时(实际上也只处理一次,毕竟第一次处理完就算reachable了),依旧是先处理其new,assign语句

addedge与之前相同:

ProcessCall
该函数实际上就是实现call 语句的Rule
1.找到目标方法(Dispatch)
2.传目标方法
3.传参
4.传返回值
dispatch是根据类型找类的,所以可能会发生第一次遇到的oi但是边已经处理过的情况,所以需要判断,避免冗余计算
建立call graph是在add 边到CG处建立的(第一次遇到该边的时候)

L是callsite语句,在多次调用ProcessCall的时候可能会重复分析同一条L语句,因为一个变量x的pt(x)发生变化时都会触发一次ProcessCall而L对于一个特定的x是固定不变的

这是目前为止第一个完整的全过程分析算法,输出:pt,CG
示例
过程建议看视频

Static Analysis for Security
保密性:信息泄漏,读保护
完整性:信息篡改(污染),写保护(防止低->高),如sql注入等
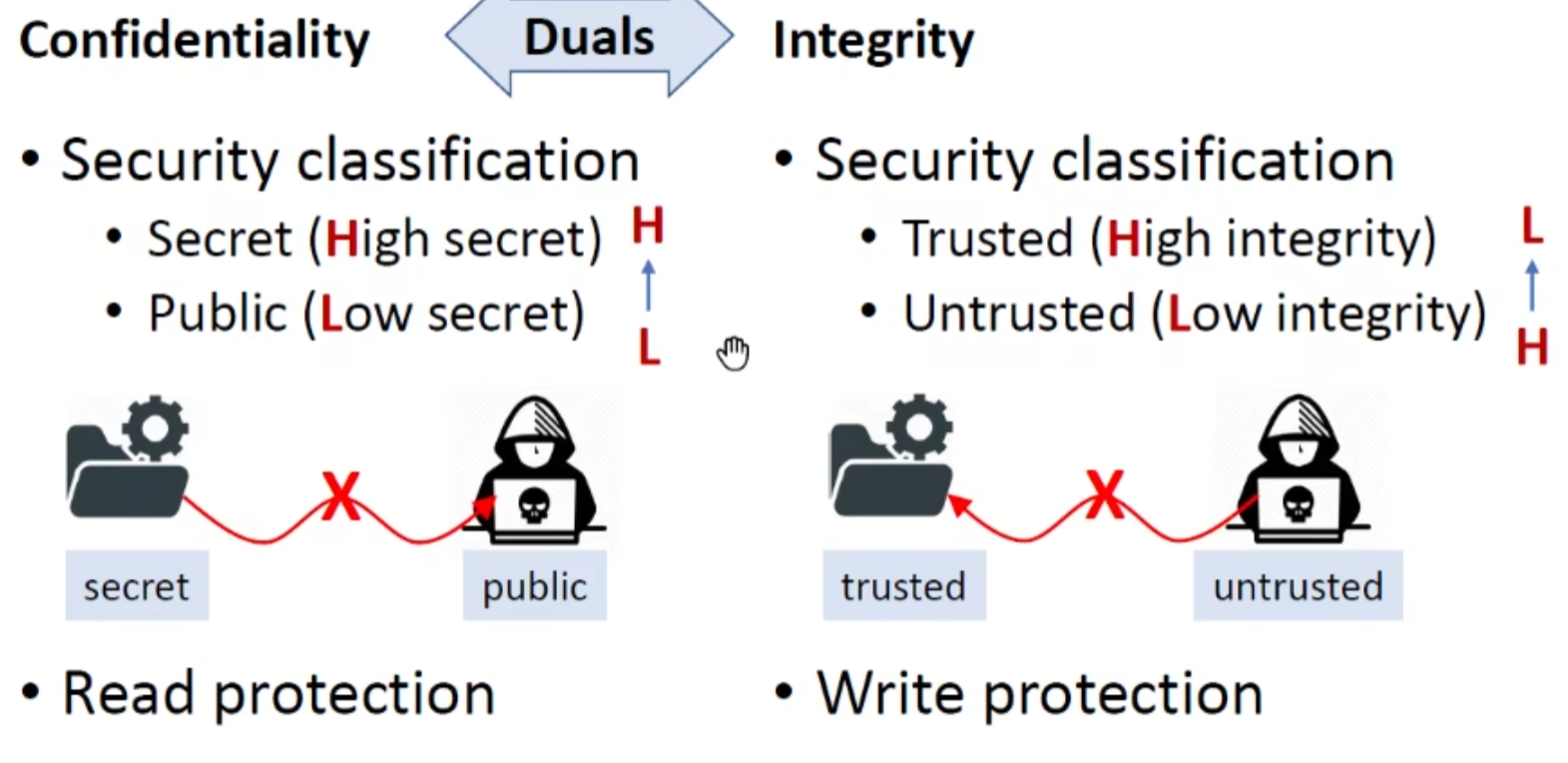
完整性需要确保准确性、完全性、一致性,即数据不被破坏,存储了所有的数据,数据的发送/接受是一致的
隐藏信道(Covert/Hidden Channels)
没有数据流也可以泄露信息,有点侧信道攻击的意思

一些能推断出secret可能是负数的隐藏信道例子:

污点分析(Taint Analysis)
思路:将程序中的数据分为两类
1.污点数据,有标记/有意义的数据(如用户输入的不可信数据,或保密的数据 )
2.普通数据
从污点数据的源头开始分析其流向,判断它是否会流向sink(一些敏感的方法,如泄露或代码执行),本质上和指针分析十分相似

应用:分别对应完整性(如执行注入的恶意代码)和保密性(如泄露敏感信息)

借助指针分析来实现污点分析

拓展指针分析的域
多了污点数据集合

输入/输出
输入
1.由于只关注污点数据,故sources只需要关注与污点数据有关的方法
2.关注的特定流向sinks(敏感方法集合)
输出:
污点流:污点数据以及sink方法的pair集合(污点数据流向sink方法)
Rules
sink&&source处理

方法处理(我们关注的是显示流)
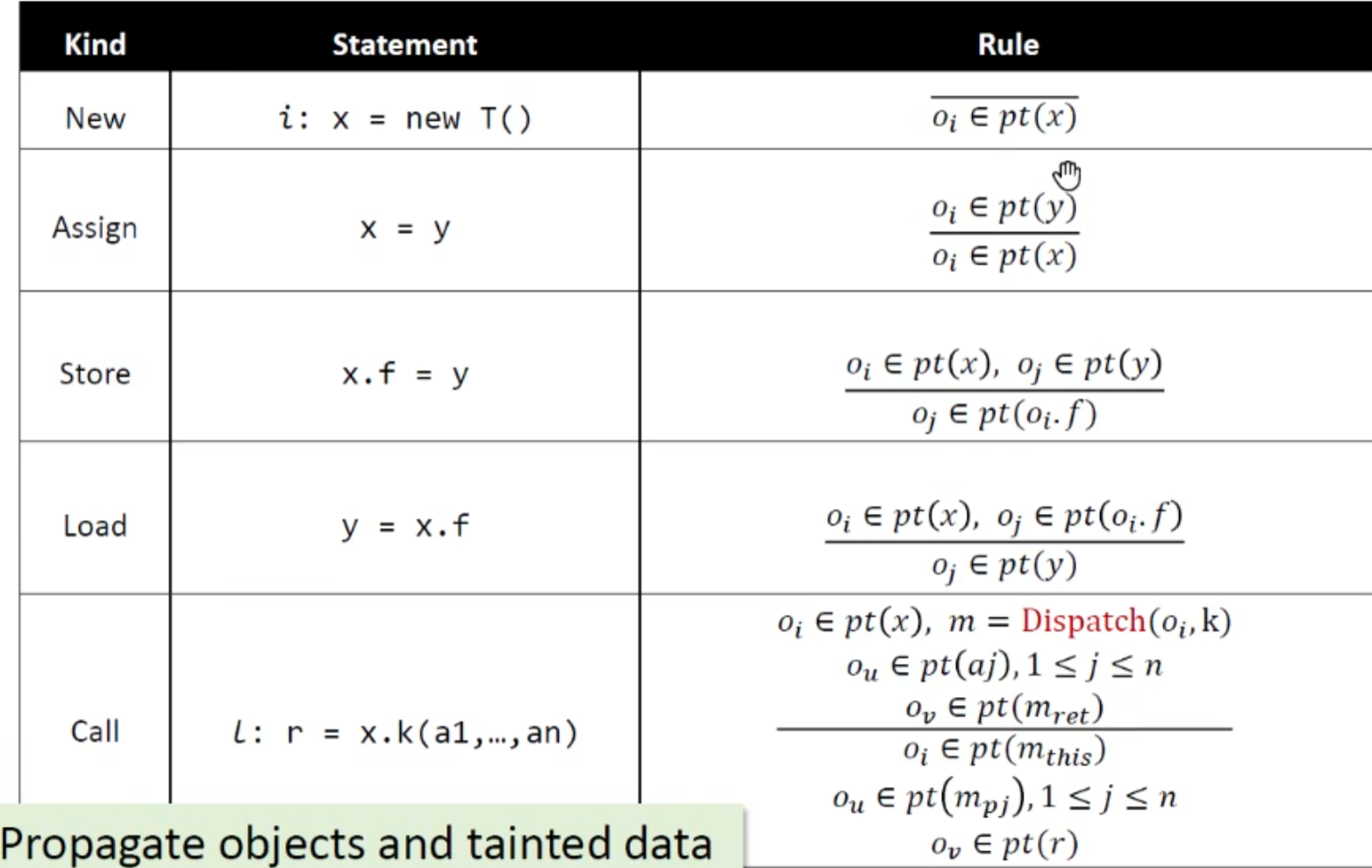
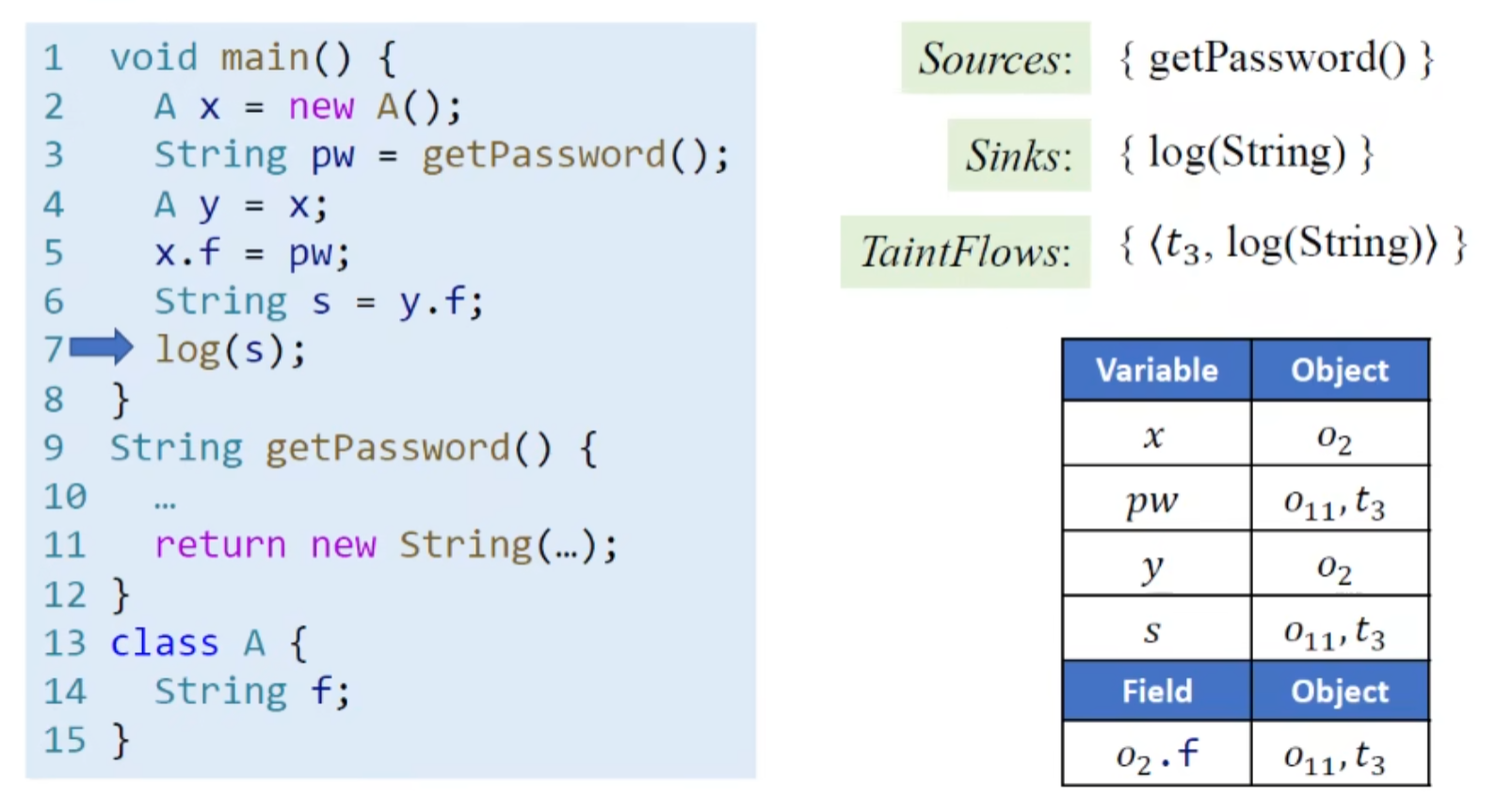
示例
log为写日志行为,存在泄露
(注意这里是上下文不敏感的分析)
分析器:c++用llvm,java用soot,wala,也有一些拿datalog实现
Datalog
命令式语言(imperative):常见编程语言如c类语言,java,go等
声明式语言(declarative):如sql语言